The angle of elevation of the top of a vertical tower from two points distance a and b from the base and in the same line with it, are complimentary .If θ is the angle subtended at the top of the tower by the line joining these points then sin θ =
a−b√2(a+b)
a+ba−b
a−ba+b
none of these
The correct Answer is:C
Step by step video, text & image solution for The angle of elevation of the top of a vertical tower from two points distance a and b from the base and in the same line with it, are complimentary .If theta is the angle subtended at the top of the tower by the line joining these points then sin theta = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - OBJECTIVE RD SHARMACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise
45 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
- INCREASING AND DECREASING FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - INCREASING AND DECREASING FUNCTIONSEXERCISE - Chapter Test
20 Videos
Similar Questions
The angles of elevatio of the top of a tower from two points 8 m and 32 m from the base and in the same straight line with it are complementary. Find the heigt of the tower.
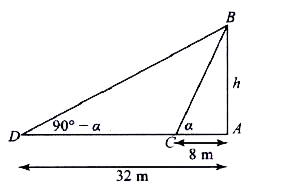
View SolutionThe angles of elevation of the top of a tower from two points situated at distances 36m and 64m from its base and in the same straight line with it are complementary. What is the heigth of the tower
View Solution
Knowledge Check
If the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
A√abB√abC√a+bD√a−bThe angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is
A5mB15mC5√2mD75mThe angles of elevation of the top of a tower from two points on the ground at distances 32 m and 18 m from its base and in the same straight line with it are complementary. The height(in m) of the tower is .....
A24B20C28D16
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View SolutionThe angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is :
View Solution
