The angles A, B and C of a triangle ABC are in arithmetic progression. AB=6 and BC=7. Then AC is :
√41
√39
√42
√43
The correct Answer is:D
To solve the problem step by step, we will follow the reasoning outlined in the video transcript.
1. Understanding the Problem:
We are given a triangle ABC where the angles A, B, and C are in arithmetic progression. The lengths of sides AB and BC are given as 6 and 7, respectively. We need to find the length of side AC.
2. Setting Up the Angles:
Since the angles are in arithmetic progression, we can express them as:
- Angle A = A - D
- Angle B = A
- Angle C = A + D
Here, A is the middle angle and D is the common difference.
3. Using the Sum of Angles in a Triangle:
The sum of the angles in a triangle is 180 degrees. Therefore, we can write:
(A−D)+A+(A+D)=180
Simplifying this gives:
3A=180
Thus, we find:
A=60 degrees
4. Finding the Other Angles:
Since A = 60 degrees, we can express angles B and C:
- Angle B = 60 degrees
- Angle C = 60 + D
- Angle A = 60 - D
However, we need to find the value of D to determine angles B and C.
5. Using the Cosine Rule:
We will apply the cosine rule to find the length of side AC (let's denote it as a):
cosA=b2+c2−a22bc
Here, b=BC=7, c=AB=6, and A=60 degrees.
6. Calculating Cosine of Angle A:
We know:
cos60∘=12
Substituting into the cosine rule gives:
12=72+62−a22⋅7⋅6
7. Substituting Values:
Now, substituting the values:
12=49+36−a284
8. Cross-Multiplying:
Cross-multiplying gives:
42=49+36−a2
9. Simplifying:
Simplifying this equation:
42=85−a2
Rearranging gives:
a2=85−42=43
10. Finding the Length of AC:
Taking the square root gives:
a=√43
Final Answer:
The length of side AC is √43.
We are given a triangle ABC where the angles A, B, and C are in arithmetic progression. The lengths of sides AB and BC are given as 6 and 7, respectively. We need to find the length of side AC.
Since the angles are in arithmetic progression, we can express them as:
- Angle A = A - D
- Angle B = A
- Angle C = A + D
Here, A is the middle angle and D is the common difference.
The sum of the angles in a triangle is 180 degrees. Therefore, we can write:
(A−D)+A+(A+D)=180
Simplifying this gives:
3A=180
Thus, we find:
A=60 degrees
Since A = 60 degrees, we can express angles B and C:
- Angle B = 60 degrees
- Angle C = 60 + D
- Angle A = 60 - D
We will apply the cosine rule to find the length of side AC (let's denote it as a):
cosA=b2+c2−a22bc
Here, b=BC=7, c=AB=6, and A=60 degrees.
We know:
cos60∘=12
Substituting into the cosine rule gives:
12=72+62−a22⋅7⋅6
Now, substituting the values:
12=49+36−a284
Cross-multiplying gives:
42=49+36−a2
Simplifying this equation:
42=85−a2
Rearranging gives:
a2=85−42=43
Taking the square root gives:
a=√43
The length of side AC is √43.
Topper's Solved these Questions
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
14 Videos
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-3 : Comprehension Type Problems
12 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- STRAIGHT LINES BOOK - VK JAISWAL ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems
10 Videos
Similar Questions
Knowledge Check
In a right-angled triangle ABC, right angled at B, an altitude BD is dropped on AC. If AB=8 and BC=6, what is the length of AD?
A2.4B3.6C4.8D6.4
The angles A, B and C of a ΔABC are in A.P. If AB=6,BC=7,then AC=
View SolutionIf the lengths of the sides of a right- angled triangle ABC, right angled at C, are in arithmetic progression, then the value of 5(sinA+sinB) is
View SolutionThe sides AB and AC of a triangle ABC are produced, and the bisectors of the external angles at B and C meet at P. Prove that if AB>AC, then PC>PB.
View SolutionThe angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at point D. If BD=9cm and DC = 7 cm, calculate the length of AB.
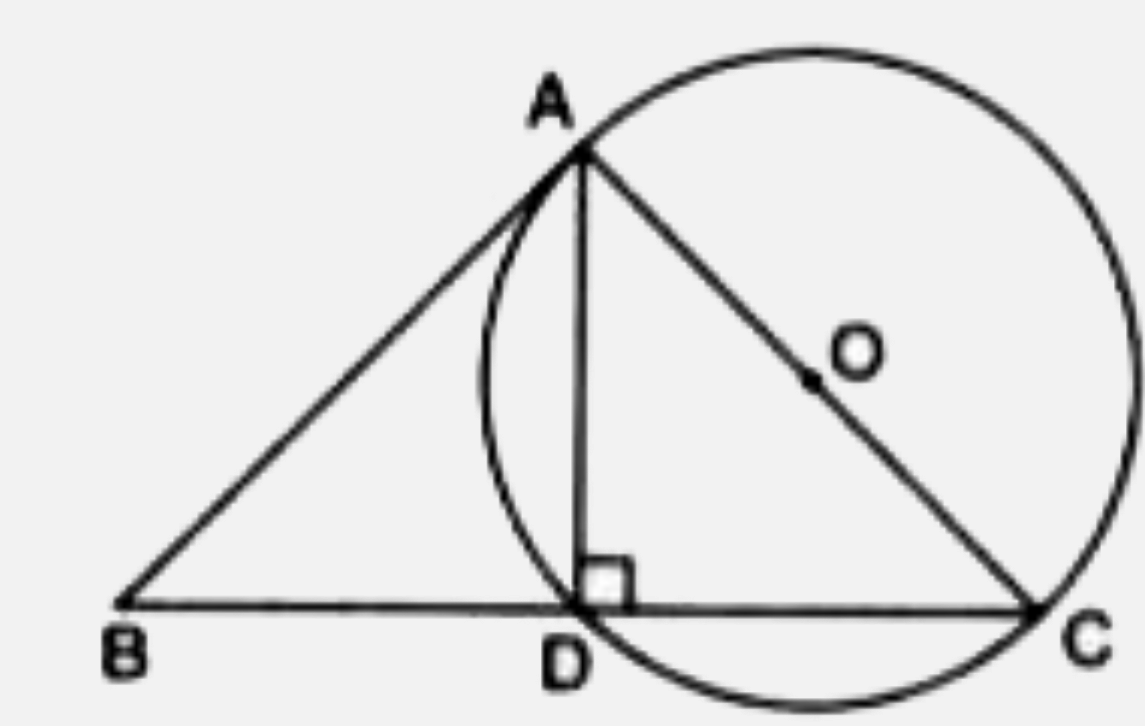
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If BC=6,AC=8, then the length of side AB is equal to
View SolutionConstruct a right angled triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
View SolutionConstruct a triangle ABC in which BC = 7cm, ∠B=75∘ and AB + AC = 13 cm.
View Solution
