The area bounded by the curves $y = cos x$ and $y = sin x$ between the ordinates $x = 0$ and $x = \frac{3 π}{2}$ is

A

$4 \sqrt{2} - 1$

B

$4 \sqrt{2} + 1$

C

$4 \sqrt{2} - 2$

D

$4 \sqrt{2} + 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Required area A is given by
$A 3 π / 2 \int 0 | cos x - sin x | d x$

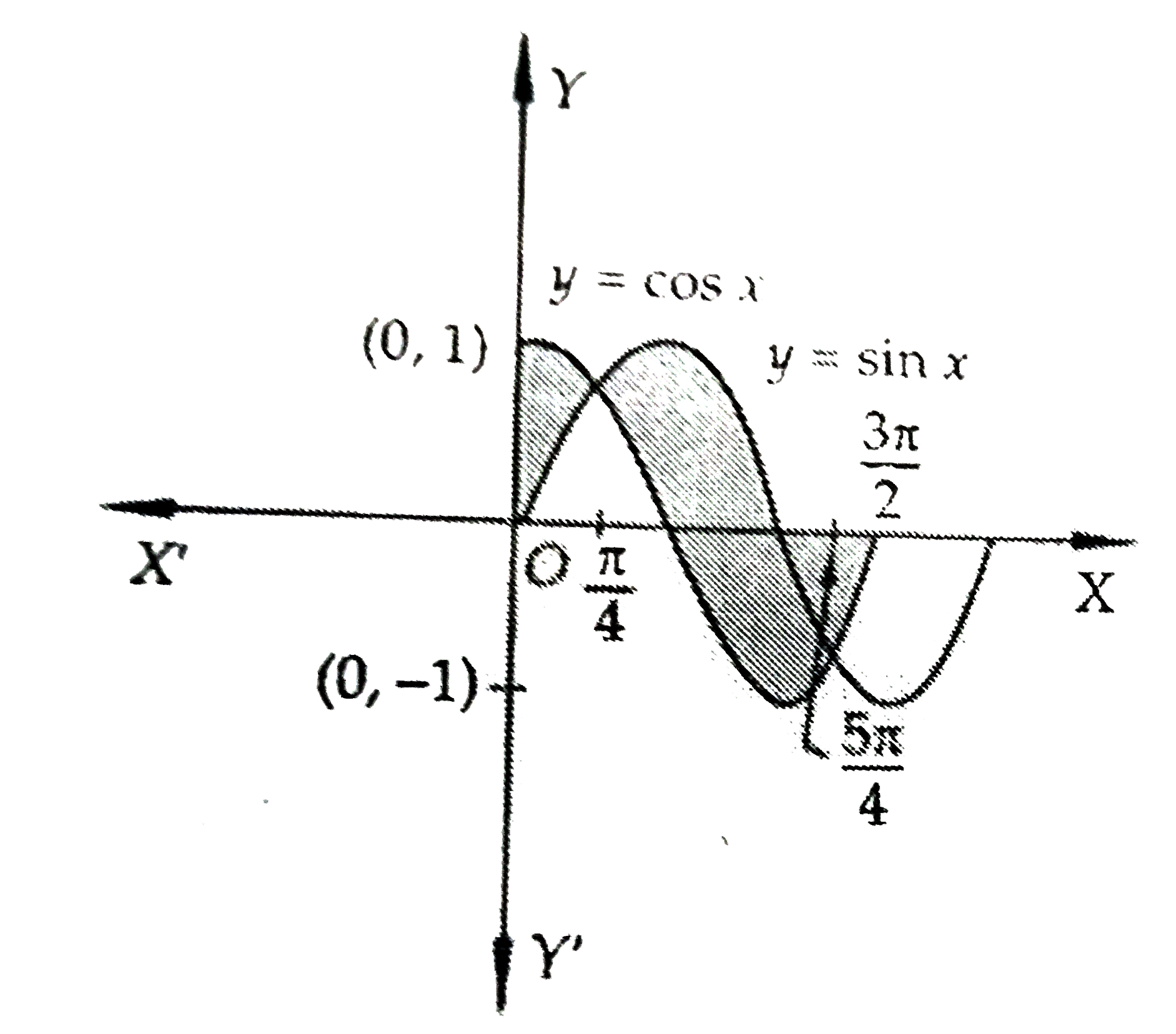
$\Rightarrow A = π / 4 \int 0 | cos x - sin x | d x + 5 π / 4 \int π / 4 | cos x - sin x | d x + 3 π / 2 \int 5 π / 4 | cos x - sin x | d x$
$\Rightarrow A = π / 4 \int 0 (cos x - sin x) d x + 5 π / 4 \int π / 4 (sin x - cos x) d x + 3 π / 2 \int 5 π / 4 (cos x - sin x) d x$
$\Rightarrow A = {[sin x + cos x]}_{0}^{π / 4} + {[- cos x - sin x]}_{π / 4}^{5 π / 4} + {[sin x + cos x]}_{5 π / 4}^{3 π / 2}$
$\Rightarrow A = (\sqrt{2} - 1) + (\sqrt{2} + \sqrt{2}) + (- 1 + \sqrt{2}) = 4 \sqrt{2} - 2$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Choose the most appropriate options.
The area bounded by the curves y =cos x and y = sin x between the ordinates x=0 and $x = \frac{3 π}{2}$ is
A $4 \sqrt{2} - 1$
B $4 \sqrt{2} + 1$
C $4 \sqrt{2} - 2$
D $4 \sqrt{2} + 2$
Question 2 - Select One
The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and $x = \frac{3 π}{2}$ , is
A $4 \sqrt{2} + 1$
B $4 \sqrt{2} - 1$
C $4 \sqrt{2} + 2$
D $4 \sqrt{2} - 2$
Question 3 - Select One
The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and $x = \frac{3 π}{2}$ , is
A $(4 \sqrt{2} - 2)$ sq units
B $(4 \sqrt{2} + 2)$ sq units
C $(4 \sqrt{2} - 1)$ sq units
D $(4 \sqrt{2} + 1)$ sq units

OBJECTIVE RD SHARMA-AREAS OF BOUNDED REGIONS-Chapter Test

Home
Ask Doubt
Profile