The area bounded in the first quadrant by the normal at $(1, 2)$ on the curve $, y^{2} = 4 x, x -$ axis &the curve is given by (A) $\frac{10}{3}$ (B) $\frac{7}{3}$ (C) $\frac{4}{3}$ (D) $\frac{9}{2}$

A

10/3

B

$7 / 3$

C

$4 / 3$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation of normal at (1, 2 ) is $x + y = 3,$ which meets X -axis at $N (3, 0)$
$∴ Q N = 2, P Q = 2$

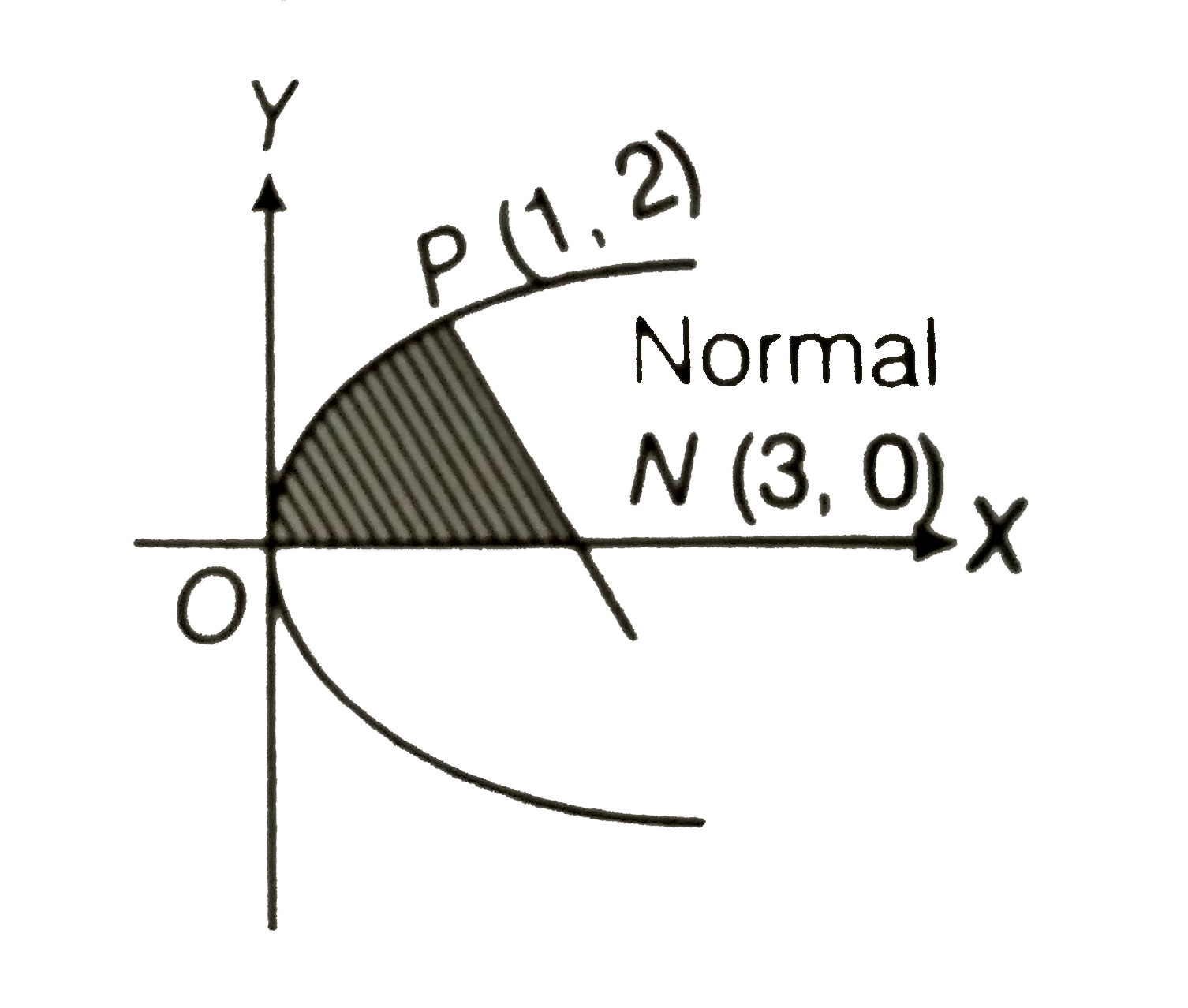
$∴$ Required area
= Area of $Δ P Q O$ + Area of $Δ P Q N$
$= \int_{0}^{1} \sqrt{(4 x)} d x + \frac{1}{2} \cdot 2 \cdot 2 = \frac{10}{3}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area lying in the first quadrant and bounded by the curve $y = x^{3}$ and the line $y = 4 x .$
A2
B3
C4
D5
Question 2 - Select One
What is the area bounded by the curve $y = 4 x - x^{2} - 3$ and the x-axis?
A $4 / 3$
B $3 / 4$
C7
D $3 / 2$
Question 3 - Select One
The area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the line $x = \sqrt{3} y$ is :
A $\frac{π}{3}$
B $\frac{π}{2}$
C $π$
D $\frac{π}{5}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 15-PAPER 2 (MATHEMATICS)

Home
Ask Doubt
Profile