The area (in sq units) of the region bounded by the curve y=√x and the lines y=0,y=x−2, isSolution in Bengali
52
5912
32
73
The correct Answer is:A
x≥0 is the region of first quadrant and fourth quadrant.
x+y≤3 is half the region of the plane divided by the line
x+y=3 where origin lies.
x2≤4y is the region inside the parabola x2=4y
y≥1+√x is the region inside the parabola y=1+√x, which has vertex at (0,1).
So, the required region is as shown in the following figure.
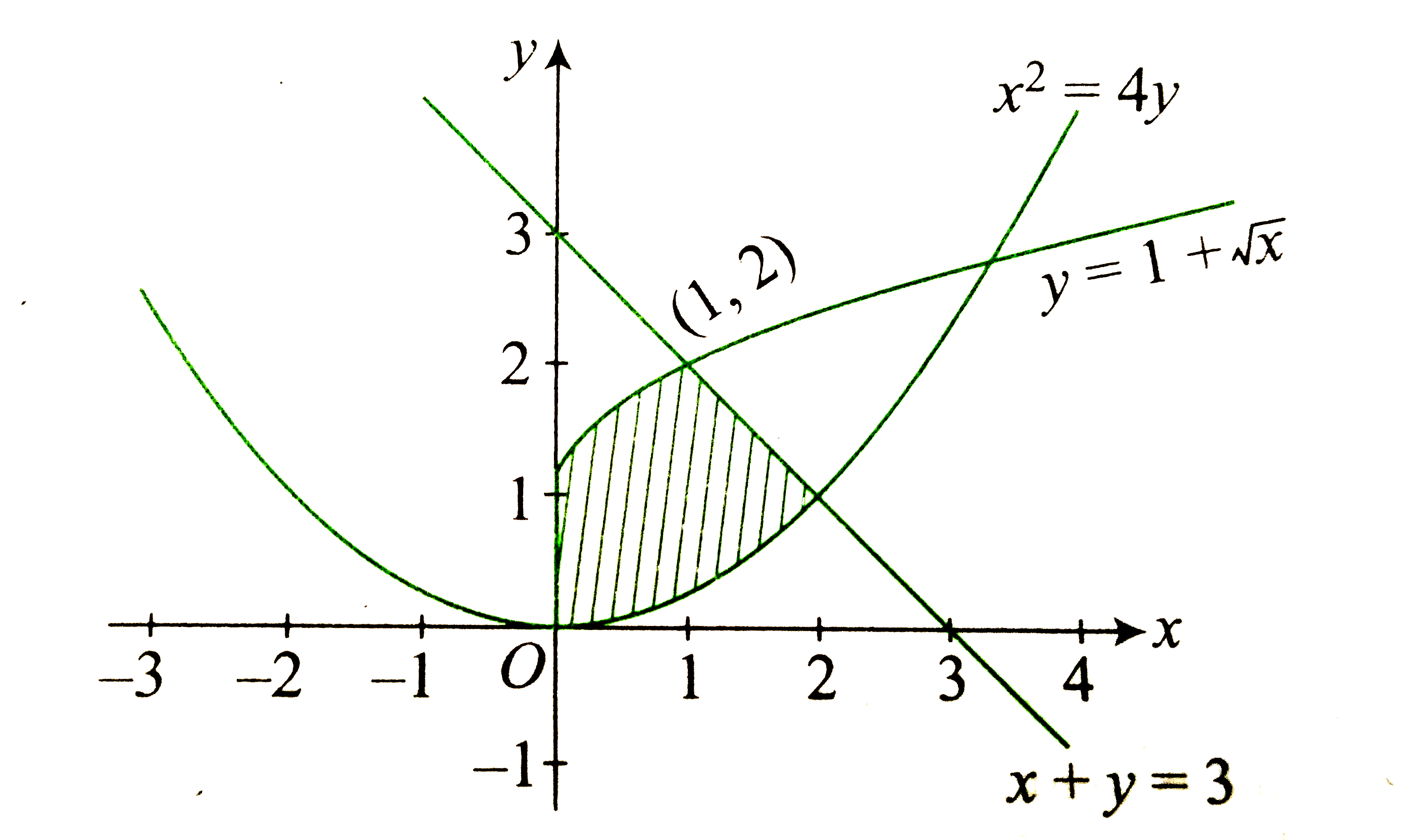
From the figure,
area =1∫0(1+√x)dx+2∫1(3−x)dx−2∫1x24dx=52
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Single Correct Answer Type30videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answer Type3videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Numerical Value Type18videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Let the straight line x= b divide the area enclosed by y=(1−x)2,y=0,andx=0 into two parts R1(0≤x≤b)andR2(b≤x≤1) such that R1−R2=14. Then b equals
03:12View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
04:00View SolutionThe area enclosed by the curve c:y=x√9−x2(x≥0) and the x-axis is________
03:23View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
02:33View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is02:24View SolutionThe area (in sq units) of the region bounded by the curve y=sqrt(x) and the lines y=0,y=x-2, is
03:10View SolutionThe area of the plane region bounded by the curve x=y2−2 and the line y = - x is (in sq units)
04:46View SolutionThe area (in sq. units) of the region bounded by the curves y=2−x2andy=|x| is k, then the value of 3k is
06:45View SolutionThe area of the region bounded by the curves : y=x2 and y=4x−x2 in sq. units is :
02:35View SolutionThe area of the region bounded by the curves y=x2 and y=4x−x2 in sq units is
02:40View SolutionThe area of the region bounded by the curves y=x3,y=1x,x=2 and x - axis (in sq. units) is
02:35View SolutionThe area (in sq units) of the region bounded by the curve y=√x and the lines y=0,y=x−2, is
03:39View SolutionThe area of the region bounded by the curve y=logex,x=0andy≤0 and X- axis is …sq. unit
11:05View SolutionThe area of the region bounded by the curve y=2√x and lines x=0 and x=1 is …Sq. units
06:55View SolutionThe area of the region bounded by the curve y=|x−5|, X- axis and the lines x=0,x=1 is …..Sq . Units.
07:28View SolutionThe Area of the region bounded by the curve y2=2x, y-axis and line y=3 is …..Sq. units
View Solution

