The area (in square units) bounded by the curves y=√x,2y−x+3=0, x-axis, and lying in the first quadrant is
9
36
18
27/4
The correct Answer is:A
Required area A is given by
A=3∫0(x2−x1)dy
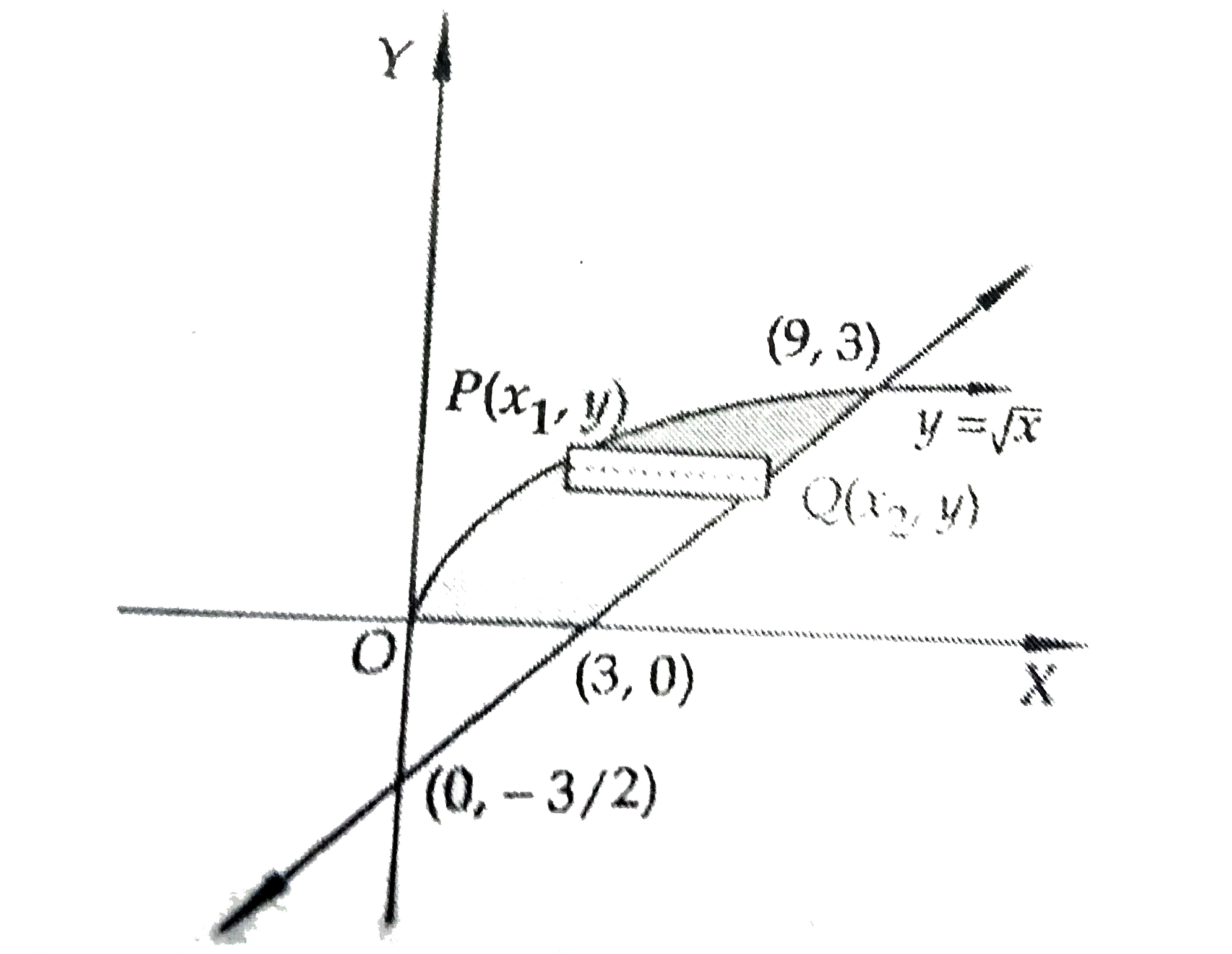
⇒A=32y+3−y20dy[y2+3y−y33]30=9+9−9=9
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
61 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
Similar Questions
The area (in square units) bounded by the curve y2=8xandx2=8y, is
View SolutionThe area bounded by the curves x+y=2 and y=x2 above x-axis in the first quadrant is ,
View SolutionThe area (in sq. units) of the region bounded by the curves y=2x and y=|x+1|, in the first quadrant is :
View SolutionArea (in square units) of the region bounded by the curve y2=4x,y-axis and the line y=3 , is
View SolutionThe area in square units bounded by the curves y=x3,y=x2 and the ordinates x=1,x=2 is
View SolutionThe area (in square units), bounded by y=2−x2 and x+y=0 , is
View SolutionThe area (in square units) bounded by curves y=sinx between the ordinates x=0, x=π and the x-axis , is
View SolutionThe area bounded by the curves y=√x,2y+3=x, and x-axis in the 1st quadrant is (A) 18 sq. units (B) 274 sq.units (C) 43 sq.units (D) 9 sq. units
View SolutionThe area (in sq. units) bounded by the curve exy−2=0 with the x - axis from x = 0 to x = ln 2 is
View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
View Solution
