The area of a square is equal to the area of a circle. The ratio between the side of the square and the radius of the circle is (a) (b) (c) (d)
To solve the problem, we need to find the ratio between the side of a square and the radius of a circle, given that their areas are equal. Let's break down the solution step by step.
Step 1: Understand the areas of the square and the circle
The area of a square (A_s) is given by the formula:
As=s2
where s is the side length of the square.
The area of a circle (A_c) is given by the formula:
Ac=πr2
where r is the radius of the circle.
Step 2: Set the areas equal to each other
According to the problem, the area of the square is equal to the area of the circle:
s2=πr2
Step 3: Rearrange the equation to find the ratio
We want to find the ratio sr. To do this, we can rearrange the equation from Step 2:
s2r2=π
Step 4: Take the square root of both sides
To find sr, we take the square root of both sides:
sr=√π
Step 5: Write the ratio in the required format
The ratio of the side of the square to the radius of the circle can be expressed as:
s:r=√π:1
Conclusion
Thus, the ratio between the side of the square and the radius of the circle is:
Option (a): √π:1
---
The area of a square (A_s) is given by the formula:
As=s2
where s is the side length of the square.
Ac=πr2
where r is the radius of the circle.
According to the problem, the area of the square is equal to the area of the circle:
s2=πr2
We want to find the ratio sr. To do this, we can rearrange the equation from Step 2:
s2r2=π
To find sr, we take the square root of both sides:
sr=√π
The ratio of the side of the square to the radius of the circle can be expressed as:
s:r=√π:1
Thus, the ratio between the side of the square and the radius of the circle is:
Option (a): √π:1
Topper's Solved these Questions
Similar Questions
If the area of a square is same as the area of the circle, then the ratio of their perimeters, in terms of π , is (a) π :√3 (b) 2 :√π (c) 3 :π (d) π :√2
View SolutionIf the diameter of a circle is equal to the diagonal of a square, then the ratio of their areas is (a)7:1 (b) 1:1 (c)11:7 (d) 22:7
View Solution
Knowledge Check
What is the radius of a circle with an area of π4?
A0.2B0.4C0.5D2.0If the area of a circle is 64π, which is the circumference of the circle?
A8πB16πC32πD64πWhat is the area of the circle whose radius is the average of the radii of two circles with areas of 16πand100π?
A25πB36πC49πD64π
A circle is inscribed in a square of side 14 m. The ratio of the area of the circle and that of the square is (a)π:3 (b) π:4 (c)π:2 (d) π:1
View SolutionABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is (a) 2−√2 (b) √2−1 (c) √2−12 (d) 1√2
View SolutionThe ratio of the perimeter (circumference) and diameter of a circle is
(a)π
(b) 2π
(c)π2
(d) π4
View SolutionThe ratio of the area of a square of side a and that of an equilateral triangle of side a, is (a) 2:1 (b) 2:√3 (c) 4:3 (d) 4:√3
View Solution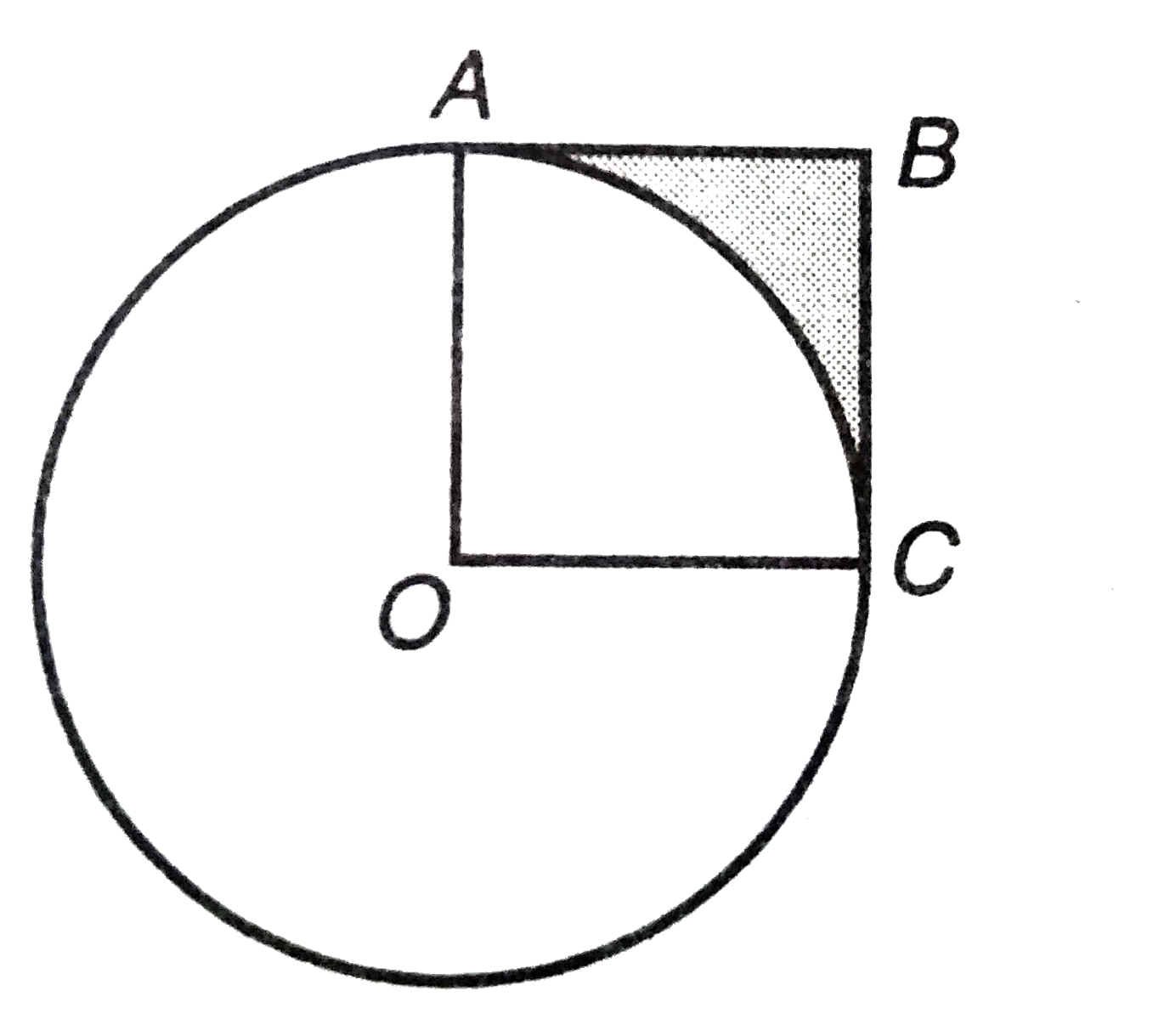
In the figure above, OABC is a square. If the area of circle O is 2π, what is the area of the shaded region?
View Solution