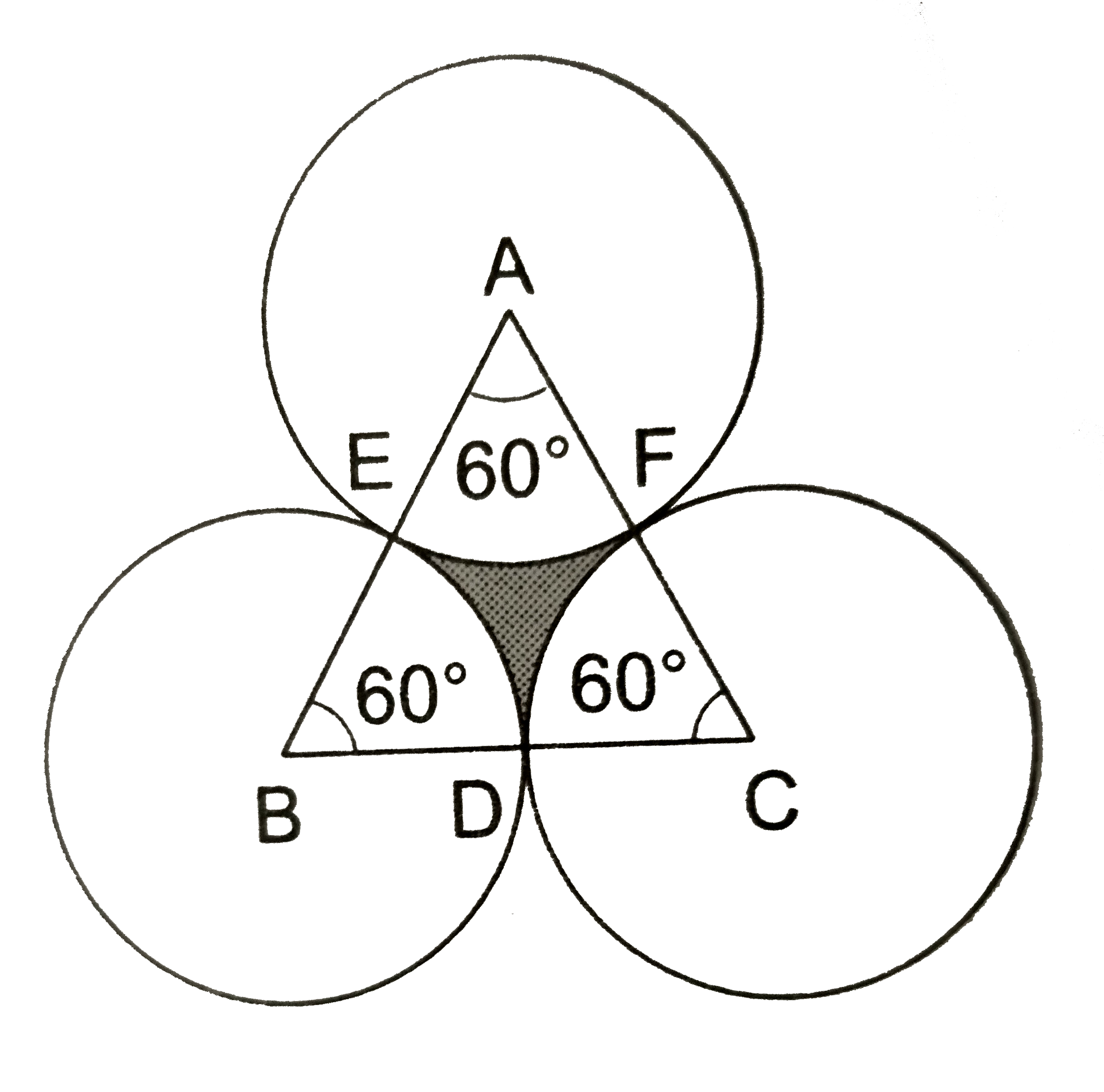
The area of an equilateral triangle ABC is 17320. 5\ c m^2. With each

The area of an equilateral triangle is $4 \sqrt{3} c m^{2} .$ . Find the length of each side of the triangle
A3 cm
B $2^{2}$ cm
C $2 \sqrt{3} c m$
D4 cm
Find the area of an equilateral triangle whose sides are 12 cm.
Aa) $29 \sqrt{5}$
Bb) $45 \sqrt{2}$
Cc)38
Dd) $36 \sqrt{3}$
Find the area of equilateral triangle whose each side is 20 cm.
A $\frac{100}{\sqrt{3}} c m^{2}$
B $100 \sqrt{3} c m^{2}$
C $100 \frac{\sqrt{3}}{2} c m^{2}$
D100 (sqrt(3))/(4)

The area of an equilateral triangle ABC is $17320.5 c m^{2}$ . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (U