Question

The area of the quadrilateral formed by the tangents at the endpoint of
the latuc rectum to the ellipse ${\displaystyle \frac{x^2}{9}+\frac{y{0}^2}{5}=1}$
is
27/4 sq. unit (b) 9 sq. units
27/2 sq. unit
(d) 27 sq. unit

Options

A. `27//4` sq units
B. 9 sq. units
C. `27//2` sq .units
D. 27 sq.units

Explanation

The given ellipse is
`(x^(2))/(9)+(y^(2))/(5)=1`
Then , `a^(2)=9,b^(2)=5`. Therefore,
`e=sqrt(1-(5)/(9))=(2)/(3)`
The equation of tangent at L is `(2x)/(9)+(y)/(3)=1`
The tangent meets rthe x-axis at A(9/2,0) and the y-axis at B(0,3) . Therefore,
Area of `DeltaOAB=(1)/(2)xx(9)/(2)xx3=(27)/(4)`

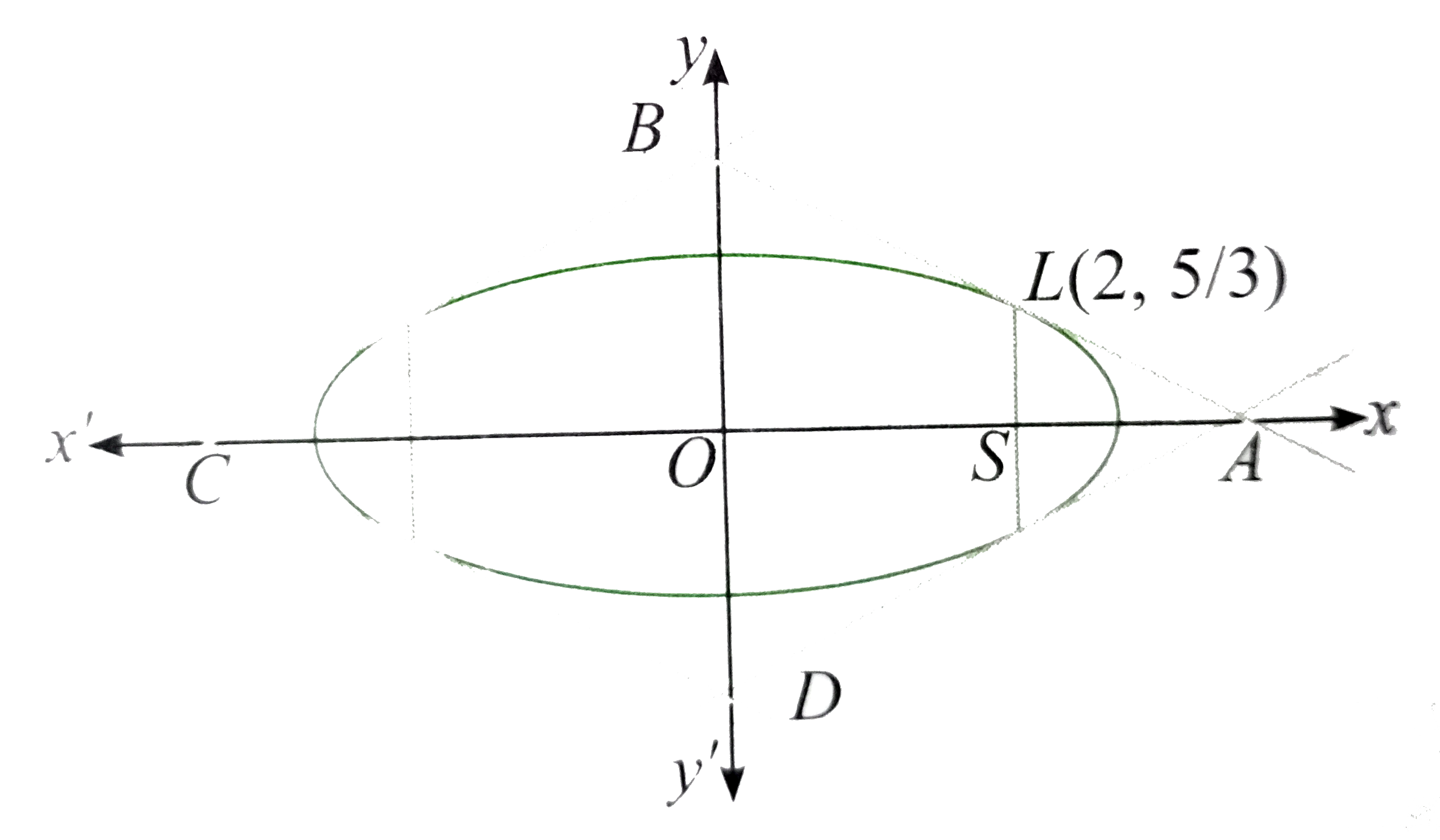
By symmetry,
Area of quadrilateral `=4xx("Area of " DeltaOAB)`
`=4xx(27)/(4)=27` sq. units