The area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is
3
6
9
12
The correct Answer is:c
The equation of the parabola is y2−4y−x+5=0
The equation of tangent at (2,3) is
3y−2(y+3)−(x+2)2+5=0or,2y−x−4=0
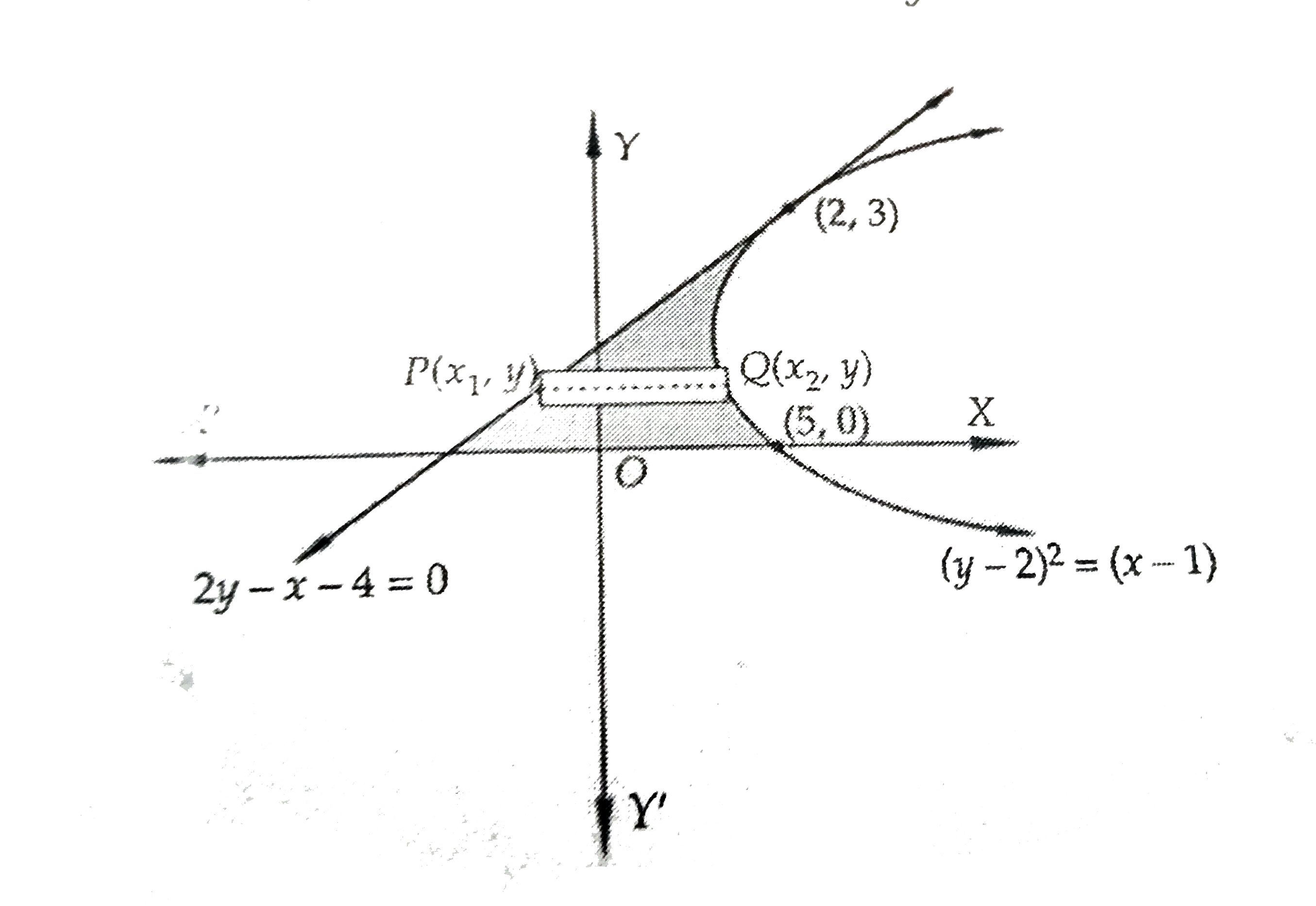
∴ Required area A is given by
A=3∫0(x2−x1)dx
⇒A=3∫0[{(y−2)2+1}−{2y−4}]dy
⇒A=2∫0(y2−6y+9)dy=3∫0(3−y)2dy=−[(3−y)33]30=9
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
62 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMACHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- APPLICATION OF DERIVATIVESBOOK - OBJECTIVE RD SHARMACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Illustration
6 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
Similar Questions
The area of the region bounded by the parabola (y2)2=x1 , the tangent to the parabola at the point (2, 3) and the xaxis is (1) 3 (2) 6 (3) 9 (4) 12
View SolutionThe area of the region bounded by the parabola (y−2)2=(x−1), the tangent to it at the point whose ordinate is 3 and the x-axis is :
View Solution
Knowledge Check
The area of the region bounded by the parabola y2=9x and the line y=3x is :
A12 sq. unitsB13 sq. unitsC14 sq. unitsD23 sq. units
Find the area of the region bounded by the parabola y2=8x and the line x=2
View SolutionFind the area of the figure bounded by the parabola y=−x2+2x+3, the line tangent to it at the point M (2,−5) and the y-axis
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x|.
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x| .
View SolutionFind the area of the region bounded by the parabola y2=2x and the line x−y=4
View SolutionThe area of the region bounded by the parabola x=−y2 and the line y=x+2 is
View SolutionFind the area of the region bounded by the parabola y2=25x and the line x =5
View Solution
