The area of the smaller segment cut off from the circle x2+y2=9 by x = 1 is
A
12(9sec−13−√8) sq unit
B
12(9sec−13−√8) sq unit
C
(√8−9sec−13) sq unit
D
None of the above
Video Solution
Text Solution
The correct Answer is:B
Required area =2∫31ydx=2∫31√9−x2dx
=2.12[x√9−x2+9sin−1.x3]31
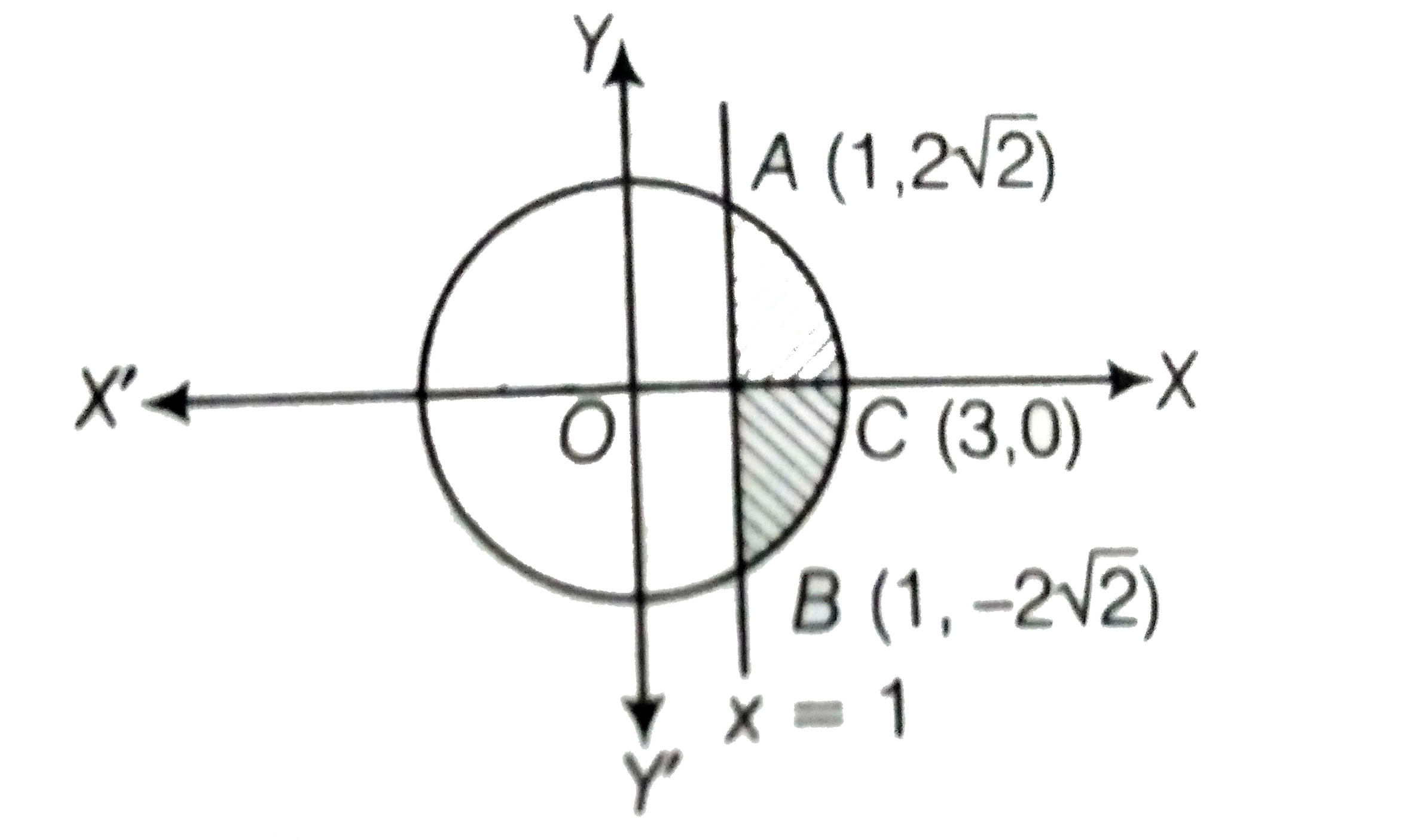
=[9sin−1(1)−√8−9sin−1(13)]=[9.π2−9sin−1(13)−√8]
=[9{cos−1(13)}−√8] [∵cos−1θ=π2−sin−1θ]
=[9sec−13−√8] sq unit
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 2
34 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
The area of the smaller segment cut off from the circle x2+y2=9 by x = 1 is
A12(9sec−13−√x)Bsec−13−√8C√8−9sec−13DNone of theseThe area of the smaller part of the circle x2+y2=2 cut off by the line x=1 is
Aπ2 sq. unitsB(π2−1) sq. unitsC(π2+1) sq. unitsD(π2−12) sq. unitsThe area of the smaller region bounded by the circle x2+y2=1 and the lines |y|=x+1 is
A(π−2)/4B(π−2)/2C(π+2)/2DNone of these
The area of the smaller portion of the circle x2+y2=4 cut off the line x+y=2 is
View SolutionFind the ara of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionArea of the segment cut off from the parabola y2=4x by the line y=8x−1 is …...........
View SolutionFind the area of the smaller part of the circle x2+y2=a2cut off by the line x=a√2
View SolutionThe area of smaller part between the circle x2+y2=4 and the line x=1 is
View Solution
