The area of trapezium field whose parallel sides are $25 c m, 13 c m$ and other sides are $15 c m and 15 c m .$

Video Solution

Text Solution

Verified by Experts

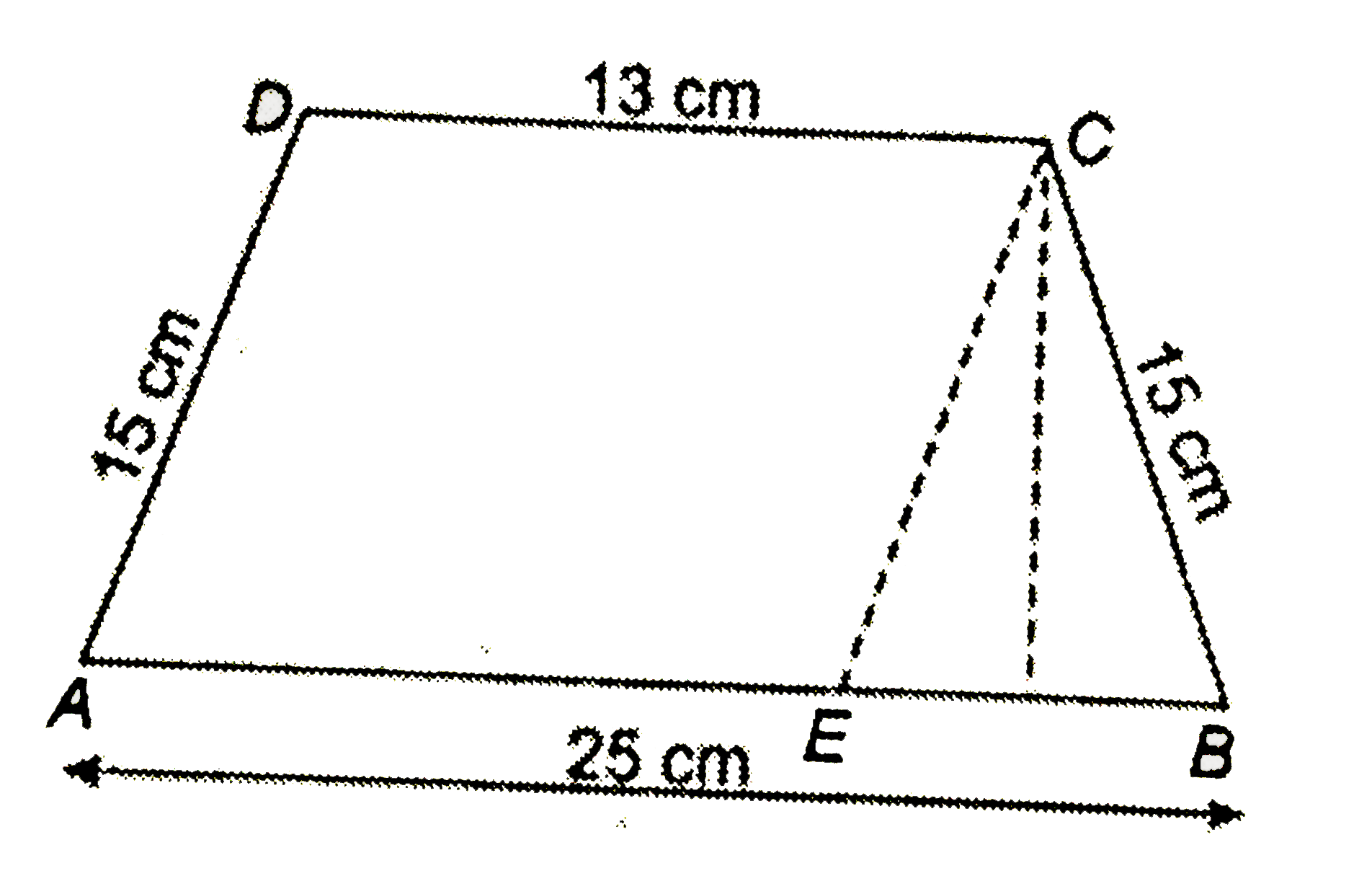
Let $A B C D$ be the given trapezium whose $A B = 25 c m, C D = 13, B C = 15 c m$ and $A D = 15 c m .$
Draw $C E ∣ ∣ A D$
Now, ADCE is a parallelogram in which AD|| CE and AE||CD.
$∴ A E = D C = 13$ cm,
and $B E = A B - A E = 25 - 13 = 12 c m$
In $Δ B C E, s = \frac{15 + 15 + 12}{2} = 21$ cm
$∴$ Area of $Δ B C E = \sqrt{s (s - a) (s - b) (s - c)}$
$= \sqrt{21 (21 - 15) (21 - 15) (21 - 12)}$
$= \sqrt{21 \times 6 \times 6 \times 9} = 18 \sqrt{21} {cm}^{2} ... (1)$
Let h be the height of $Δ B C E$ , then
Area of $Δ B C E = \frac{1}{2} (base \times height)$
$= \frac{1}{2} \times 12 \times h = 6 h (. ∵ E B = 12) ... (2)$
From (1) and (2) , we have
$6 h = 18 \sqrt{21}$
$h = 3 \sqrt{21}$ cm
The height trapezium ABCD is same as that of $Δ B C E$ .
$∴$ Area of trapezium $= \frac{1}{2} (A B + C D) \times h$
$= \frac{1}{2} (25 + 13) \times 3 \sqrt{21} = 57 \sqrt{21} {cm}^{2}$ .

|

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of a trapezium whose parallel sides are 9 cm & 16 cm and the distance between these sides is 8 cm, is
A60 $c m^{2}$
B72 $c m^{2}$
C56 $c m^{2}$
D100 $c m^{2}$

NAGEEN PRAKASHAN-HERONS'S FORMULA-Revision Exercise

Home
Ask Doubt
Profile