The arrow is rotated and it stops randomly on the disc. Find out on which colour it may stop.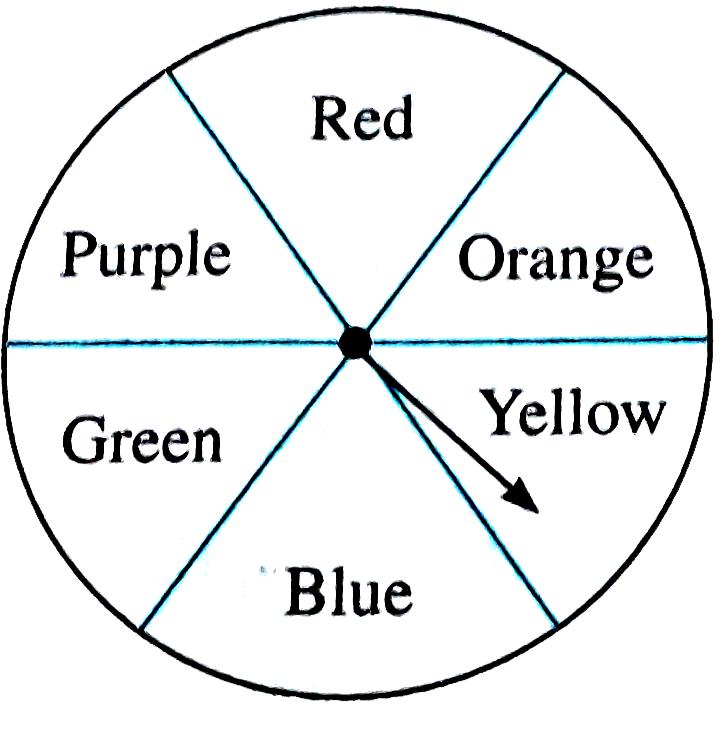 
There are six colours on the disc. The arrow can stop on any of the colours.
∴S={Red,Orange,Yellow,Blue,Green,Purple}
∴n(S)=6.
Similar Questions
If earth stops rotating
View SolutionIn Fig., shown a disc on which a player spins an arrow twice. The function ab is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction ab>1.
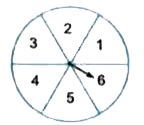View Solution
Knowledge Check
- Question 1 - Select One
A cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
AIωI+mR2BIω+mvRI+mR2CIω−mvRI+mR2DIω−mvRI - Question 2 - Select One
Blood does not stop coming out of a wound in
ATetanusBMalariaCHaemophiliaDAIDS - Question 3 - Select One
A ring and a disc of different masses are rotating with the same kinetic energy. If a retarding torque (τ) is applied to the ring, the ring stops after completing n rotations. If the same retarding torque is applied to the disc, how many rotations would it complete before coming to rest?
A2nB4nCn2Dn
A bus travels 1300 km with an average speed of 65 km/h. If it stops at 8 junctions it takes exactly 1 day to travel the whole distance. Find out the time duration it stops for at each stop.
View SolutionA man of mass m1 stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre . The man walks along the edge of the disc through angle θ relative to the disc and then stops . find the angle through which the disc turned the time the man stopped .
[2m1θ2m1+m2]View SolutionA man of mass m1 stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre. At a certain moment the man starts moving along the edge of the disc, he shifts over an angle φ′ relative to the disc and then stops. In the process of motion the velocity of the man varies with time as v′(t).
Assuming the dimensions of the man to be negligible, find:
(a) the angle through which the disc had turned by the moment the man stopped,
(b) the force moment (relative to the rotation axis) with which the man acted on the disc in the process of motion.View SolutionA disc of radius R and mass m is mounted on a vertical axis through its centre and perendicular to its plane. A rat of same mass m runs around the rim of the disc with speed v anticlockwise relative to stationary observer. The disc rotates clockwise with angular speed omega. The rat finds a piece of bread on the rim and stops. Find the angular velocity of the disc after the rat stops.
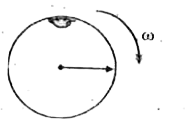View SolutionName the force which helps things to move and stop.
View Solution