The bisectors of angles A and B of a scalene triangle ABC meet at O.
OR and OQ are perpendiculars drawn to AB and CA respectively. What is the relation between OR and OQ?
To find the relation between the lengths of the perpendiculars OR and OQ drawn from the incenter O of triangle ABC to the sides AB and AC respectively, we can follow these steps:
1. Identify the Triangle and Angles:
- We have a scalene triangle ABC where all sides are of different lengths.
- The angle bisectors of angles A and B meet at point O, which is the incenter of the triangle.
2. Draw the Perpendiculars:
- From point O, draw perpendiculars OR to side AB and OQ to side AC. This means that OR ⊥ AB and OQ ⊥ AC.
3. Understanding the Incenter:
- The point O is the incenter of triangle ABC, which is the point where the angle bisectors of the triangle intersect.
- The incenter is equidistant from all three sides of the triangle.
4. Relate the Perpendiculars to the Inradius:
- The lengths OR and OQ represent the distances from the incenter O to the sides AB and AC respectively.
- Since O is the incenter, the distances from O to the sides of the triangle (i.e., OR and OQ) are equal because the incenter is equidistant from all sides of the triangle.
5. Conclusion:
- Therefore, we can conclude that OR = OQ. This means the lengths of the perpendiculars from the incenter to the sides of the triangle are equal.
Final Relation:
Thus, the relation between OR and OQ is:
OR=OQ
- We have a scalene triangle ABC where all sides are of different lengths.
- The angle bisectors of angles A and B meet at point O, which is the incenter of the triangle.
- From point O, draw perpendiculars OR to side AB and OQ to side AC. This means that OR ⊥ AB and OQ ⊥ AC.
- The point O is the incenter of triangle ABC, which is the point where the angle bisectors of the triangle intersect.
- The incenter is equidistant from all three sides of the triangle.
- The lengths OR and OQ represent the distances from the incenter O to the sides AB and AC respectively.
- Since O is the incenter, the distances from O to the sides of the triangle (i.e., OR and OQ) are equal because the incenter is equidistant from all sides of the triangle.
- Therefore, we can conclude that OR = OQ. This means the lengths of the perpendiculars from the incenter to the sides of the triangle are equal.
Thus, the relation between OR and OQ is:
OR=OQ
Topper's Solved these Questions
Similar Questions
Knowledge Check
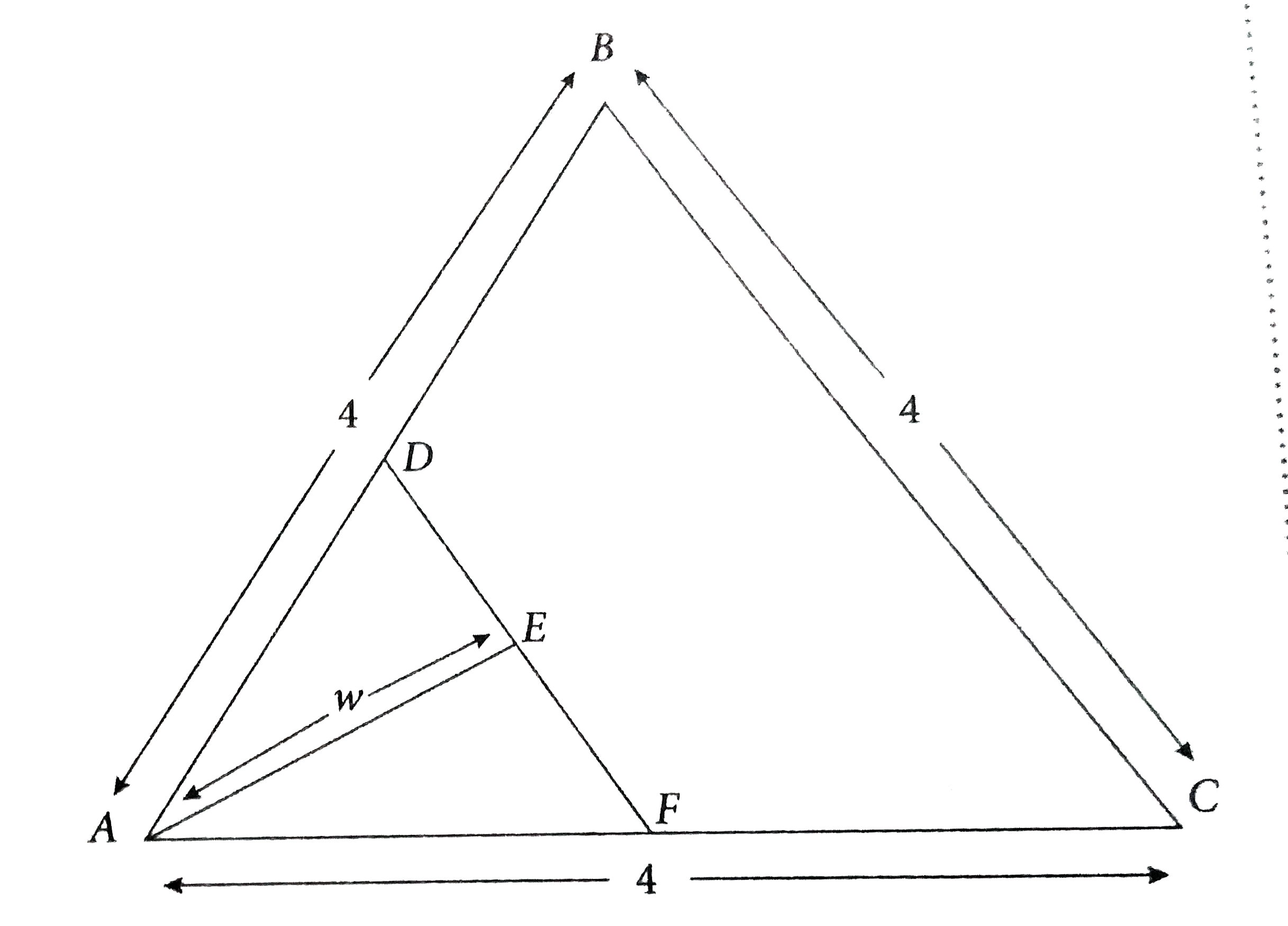
ΔABC is equilateral and ∠AEF is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?A1B√3C2D2√3
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
Does the perpendicular bisector of BC pass through O?
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What do you call the point ?
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CD×AB=CA×DE
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC ?
View SolutionThe bisectors of the acute angles of a right triangle meet at O . Find the angle at O between the two bisectors.
View SolutionBD is the disector of angle ABC. From a point P in BD, perpendiculars PE and PF are drawn to AB and BC respectively, prove that :
(i) Triangle BEP is conguent to triangle BFP (ii) PE=PF.
View Solution
