The breakdown of a sample of a chemical compounds is represented by the function p(n)=300(0.5)n, where p(n) represents the number of millligrams of the substance that remains at the end of n years. Which of the following is true?
I. 300 represents the number of milligrams of the substance that remains after the first year.
II. 0.5 represents the fraction of the starting amount by which the substance gets reduced by the end of each year.
III. Each year the substance gets reduced by one-half of 300.
I only
II only
I and III only
II and III only
The correct Answer is:B
To solve the problem, we need to analyze the function p(n)=300(0.5)n and evaluate the three statements provided.
Step 1: Evaluate Statement I
Statement I: 300 represents the number of milligrams of the substance that remains after the first year.
To check this, we need to calculate p(1):
p(1)=300(0.5)1=300×0.5=150 mg
Since p(1)=150 mg, this means that 300 mg does not represent the amount remaining after the first year.
Conclusion: Statement I is false.
Step 2: Evaluate Statement II
Statement II: 0.5 represents the fraction of the starting amount by which the substance gets reduced by the end of each year.
To verify this, we can calculate p(2):
p(2)=300(0.5)2=300×0.25=75 mg
Now, we can find the fraction of the substance that remains after the first year and the second year:
- After the first year: p(1)=150 mg
- After the second year: p(2)=75 mg
Now, we can find the fraction reduced:
Fraction reduced=1−p(2)p(1)=1−75150=1−0.5=0.5
This confirms that 0.5 does represent the fraction by which the substance is reduced each year.
Conclusion: Statement II is true.
Step 3: Evaluate Statement III
Statement III: Each year the substance gets reduced by one-half of 300.
To check this, we need to find the difference between the amounts remaining after the first and second years:
Reduction from year 1 to year 2=p(1)−p(2)=150−75=75 mg
The statement claims that the reduction is half of 300, which is:
3002=150 mg
Since the actual reduction (75 mg) is not equal to 150 mg, this statement is incorrect.
Conclusion: Statement III is false.
Final Conclusion
- Statement I: False
- Statement II: True
- Statement III: False
Thus, the only true statement is Statement II.
---
Statement I: 300 represents the number of milligrams of the substance that remains after the first year.
p(1)=300(0.5)1=300×0.5=150 mg
Since p(1)=150 mg, this means that 300 mg does not represent the amount remaining after the first year.
Statement II: 0.5 represents the fraction of the starting amount by which the substance gets reduced by the end of each year.
p(2)=300(0.5)2=300×0.25=75 mg
Now, we can find the fraction of the substance that remains after the first year and the second year:
- After the first year: p(1)=150 mg
- After the second year: p(2)=75 mg
Fraction reduced=1−p(2)p(1)=1−75150=1−0.5=0.5
This confirms that 0.5 does represent the fraction by which the substance is reduced each year.
Statement III: Each year the substance gets reduced by one-half of 300.
Reduction from year 1 to year 2=p(1)−p(2)=150−75=75 mg
The statement claims that the reduction is half of 300, which is:
3002=150 mg
Since the actual reduction (75 mg) is not equal to 150 mg, this statement is incorrect.
- Statement I: False
- Statement II: True
- Statement III: False
Topper's Solved these Questions
- PROBLEM SOLVING AND DATA ANALYSISBOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - Grib-In
40 Videos
- PROBLEM SOLVING AND DATA ANALYSISBOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - Grib-In
40 Videos
- PROBLEM SOLVING AND DATA ANALYSISBOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - EXERICSE
80 Videos
- PROBLEMS IN CONTEXT BOOK - ENGLISH SATCHAPTER - PROBLEMS IN CONTEXT EXERCISE - PRACTICE TEST
10 Videos
Similar Questions
The breakdown of sample of chemical compound is represented by the function p(t)=300(12)t, where p(t) represents the number of milligrams of the substance, and t represents the time , in years. If t=0 represents the year 2015, what will be the first year in which the amount of the substance remaining falls to cless than 5 milligrams?
View SolutionWhich of the following sequence represents atomic number of only representative elements?
View Solution
Knowledge Check
The breakdown of a 500-milligram sample of a chemical compounds in the bloodstream is represente by the function p(n)=500(0.8)n, where p(n) represents the number of milligrams of the compound that remains at the end of n hours. Which of the following is true?
I. The amount of the compound present is decreasing by a constant amount.
II. Each hour the compound gets reduced by 20% of the amount present at the beginning of that hour.
III. Each hour the compound gets reduced by 80% of 500.AI onlyBII onlyCI and III onlyDII and III onlyOne mole of N, represents which one of the following?
A28g of nitrogenB22.4 L at STPC6.022×1023N2, moleculesDAll the threeWhich of the following represents the correct graph for SN2 reaction ?
A B
B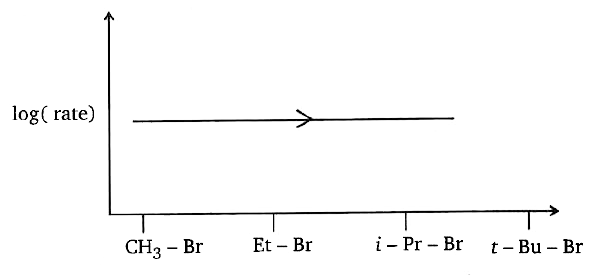 C
C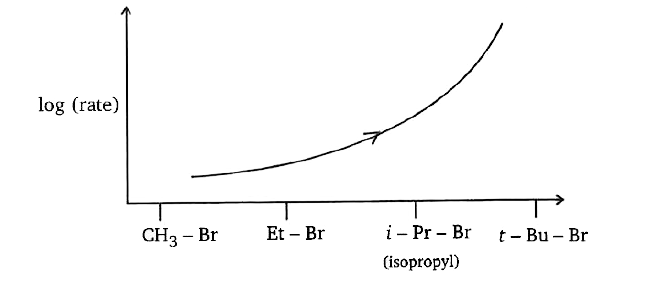 D
D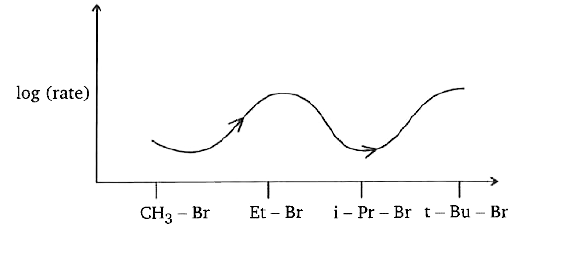
In which of the following decays n/p remains constant ?
View SolutionA radioactive substance emits n beat particles in the first 2 s and 0.5 n beta particles in the next 2 s. The mean life of the sample is
View SolutionWhich of the following graph represents correct graph for SN1 reaction :
View SolutionA radioactive substance has an initial mass of 100 grams, and its mass is reduced by 40% every 5 year. Which could be used to find the number of grams in the mass, y, that remains after x years?
View SolutionWhich of the following expressions is representative of the rate law for a SN2 reaction ?
View Solution
