The circumference of a car tire is 75 inches . About how many revolutions does this car tire make traveling 225 feet (2,700 inches ) without slipping ?
3
14
36
225
The correct Answer is:C
To find out how many revolutions a car tire makes while traveling a certain distance, we can follow these steps:
Step 1: Understand the Problem
We know that the circumference of the car tire is 75 inches. This means that for every complete revolution the tire makes, it covers a distance of 75 inches.
Step 2: Convert the Distance
The distance the car travels is given as 225 feet. We need to convert this distance into inches because the circumference is in inches.
1 foot = 12 inches, so:
225 feet=225×12 inches=2700 inches
Step 3: Calculate the Number of Revolutions
To find the number of revolutions the tire makes while traveling 2700 inches, we divide the total distance traveled by the circumference of the tire:
Number of Revolutions=Total DistanceCircumference=2700 inches75 inches
Step 4: Perform the Division
Now, we perform the division:
270075=36
Conclusion
Thus, the car tire makes 36 revolutions while traveling 225 feet (or 2700 inches).
Final Answer
The number of revolutions is 36.
---
We know that the circumference of the car tire is 75 inches. This means that for every complete revolution the tire makes, it covers a distance of 75 inches.
The distance the car travels is given as 225 feet. We need to convert this distance into inches because the circumference is in inches.
1 foot = 12 inches, so:
225 feet=225×12 inches=2700 inches
To find the number of revolutions the tire makes while traveling 2700 inches, we divide the total distance traveled by the circumference of the tire:
Number of Revolutions=Total DistanceCircumference=2700 inches75 inches
Now, we perform the division:
270075=36
Thus, the car tire makes 36 revolutions while traveling 225 feet (or 2700 inches).
The number of revolutions is 36.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The figure shows the path of a car moving around a circular recetrack . How many miles does the car travel in going from point A to Point B?
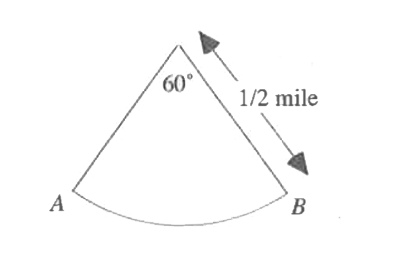 Aπ/6Bπ/3CπD30
Aπ/6Bπ/3CπD30Though there are 600 million cars on the planet, and counting, there are also seven billion people, which means that for the vast majority of us getting
around involves taking buses, ferryboats, commuter
line 5-trains, streetcars, and subways. In other words, traveling to work, school, or the market means being a straphanger: somebody who, by choice or necessity, relies on public transport, rather than a privately owned automobile.
line 10- Half the population of New York, Toronto, and London do not own cars. Public transport is how most of the people of Asia and Africa, the world’s most populous continents, travel. Every day, subway systems carry 155 million passengers, thirty-four
line 15- times the number carried by all the world’s airplanes, and the global public transport market is now valued at $428 billion annually. A century and a half after the invention of the internal combustion engine, private car ownership is still an anomaly.
line 20- And yet public transportation, in many minds, is the opposite of glamour—a squalid last resort for those with one too many impaired driving charges, too poor to afford insurance, or too decrepit to get behind the wheel of a car. In much of North
line 25- America, they are right: taking transit is a depressing experience. Anybody who has waited far too long on a street corner for the privilege of boarding a lurching, overcrowded bus, or wrestled luggage onto subways and shuttles to get to a big city airport,
line 30- knows that transit on this continent tends to be underfunded, ill-maintained, and ill-planned. Given the opportunity, who wouldn’t drive? Hopping in a car almost always gets you to your destination more quickly.
line 35- It doesn’t have to be like this. Done right, public transport can be faster, more comfortable, and cheaper than the private automobile. In Shanghai, German-made magnetic levitation trains skim over elevated tracks at 266 miles an hour, whisking people
line 40 - to the airport at a third of the speed of sound. In provincial French towns, electric-powered streetcars run silently on rubber tires, sliding through narrow streets along a single guide rail set into cobblestones. From Spain to Sweden, Wi-Fi equipped high-speed
line 45- trains seamlessly connect with highly ramified metro networks, allowing commuters to work on laptops as they prepare for same-day meetings in once distant capital cities. In Latin America, China, and India, working people board fast-loading buses that move
line 50 - like subway trains along dedicated busways, leaving the sedans and SUVs of the rich mired in dawn-to-dusk traffic jams. And some cities have transformed their streets into cycle-path freeways, making giant strides in public health and safety and ltbr line 55- the sheer livability of their neighborhoods—in the process turning the workaday bicycle into a viable form of mass transit. If you credit the demographers, this transit trend has legs. The “Millenials,” who reached adulthood
line 60 - around the turn of the century and now outnumber baby boomers, tend to favor cities over suburbs, and are far more willing than their parents to ride buses and subways. Part of the reason is their ease with iPads, MP3 players, Kindles, and smartphones: you
line 65- can get some serious texting done when you’re not driving, and earbuds offer effective insulation from all but the most extreme commuting annoyances. Even though there are more teenagers in the country than ever, only ten million have a driver’s license
line 70 - (versus twelve million a generation ago). Baby boomers may have been raised in Leave It to Beaver suburbs, but as they retire, a significant contingent is favoring older cities and compact towns where they have the option of walking and riding bikes. Seniors
line 75- too, are more likely to use transit, and by 2025, there will be 64 million Americans over the age of sixty-five. Already, dwellings in older neighborhoods in Washington, D.C., Atlanta, and Denver, especially those near light-rail or subway stations, are
line 80 - commanding enormous price premiums over suburban homes. The experience of European and Asian cities shows that if you make buses, subways, and trains convenient, comfortable, fast, and safe, a surprisingly large percentage of citizens will opt to
line 85- ride rather than drive.

What function does the third paragraph (lines 20-34) serve in the passage as a whole?AIt acknowledges that a practice favored by the author of the passage has some limitations.BIt illustrates with detail the arguments made in the first two paragraphs of the passage.CIt gives an overview of a problem that has not been sufficiently addressed by the experts mentioned in the passageDIt advocates for abandoning a practice for which the passage as a whole provides mostly favorable dataA car moving at a constant rate travels 96 miles in 2 hours. If the car maintains this rate, how many miles will the car travel in 5 hours?
A480B240C210D192
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
View SolutionA car travels 28312 km in 423 hours. How far does this car go in 1 hour, travelling at the same speed?
View SolutionA car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
View SolutionA stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the centripetal acceleration of the stone is 9.91ms−2 how many revolutions does the stone make in 20 seconds.
View SolutionAn amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is μs and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is T=(4π2μsR/g)1/2
b. Obtain a numerical value for T taking R=4.00m and μs=0.400 . How many revolations per minute does the cylinder make?
c. If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d. If instead the cylinder rate revolution is made to be somewhat smaller what happens to the magnitude and what happens to the motion of the person ?
View Solution
