The converse of the statement ''If x>y, then x+a>y+a'' is
A
If x<y, then x+a<y+a
B
If x+a>y+a, then x>y
C
if x<y, then x<y+a
D
If x>y, then x+a<y+a
Video Solution
Text Solution
The correct Answer is:B
Let p:x>y
q:x+a>y+a
p→q
Converse of the above statement is
q→p
i.e., If x+a>y+a, then x>y.
|
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - NCERT EXEMPLARCHAPTER - MATHEMATICAL REASONING EXERCISE - OBJECTIVE TYPE QUESTIONS
21 Videos
- LINEAR INEQUALITIESBOOK - NCERT EXEMPLARCHAPTER - LINEAR INEQUALITIESEXERCISE - Objective Type Questions
14 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - NCERT EXEMPLARCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Matching The Columns
5 Videos
Similar Questions
Knowledge Check
The converse of the statement:
If (x≠y) then ( x + a ≠ y +a ) isAIf (x = y) then (x + a = y + a)BIf (x ≠ y) then (x + a = y + a)CIf (x+a≠y+a) then (x≠y)DIf (x+a≠y+a) then ( x = y)Consider the following statements
I. If x and y are composite integers, so x + y is also composite.
II. If x and y are composite integers and x>y, then x - y is also a composite integer.
III. If x and y are composite integers, so also is xy.
Of the above, the correct statement is/areAOnly IIIBI and IICAll the threeDNone of theseStatement I sin−1(1√e)>tan−1(1√π)
Statement II sin−1x>tan−1y for x>y,∀x,y∈(0,1)AStatement I is True, Statement II is True, Statement II is a correct explanation for statement IBStatement I is True, Statement II is True, Statement II is NOT a correct explanation for Statement ICStatement I is True, Statement II is FalseDStatement I is False, Statement II is True.
2x−y>1,x−2y<1
View SolutionState True or False:
If x and y are integers such that x2>y2, then x3>y3.
View Solution2x−y>1,2y−x>1
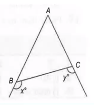
View SolutionIn the adjoining figure, x>y, Prove that AB>AC
View SolutionThe minimum value of f=x+4y subject to the constraints x+y≥8,2x+y≥10,x>0,y>0 is __________
View Solution
