The converse of the statement If , then is
(a) If then
(b) If then
(c) If then
(d) If then
The correct Answer is:B
To find the converse of the statement "If x>y, then x+a>y+a", we will follow these steps:
Step 1: Identify the original statement
The original statement can be expressed in the form of an implication:
- Let P: x>y
- Let Q: x+a>y+a
Thus, the original statement is P⟹Q.
Step 2: Write the converse
The converse of an implication P⟹Q is Q⟹P. Therefore, we need to express the converse:
- The converse will be: "If x+a>y+a, then x>y".
Step 3: Analyze the converse statement
Now we can write the converse statement clearly:
- If x+a>y+a, then x>y.
Step 4: Match with the options
Now, we need to check which of the given options matches our converse statement:
- Option A: If x<y, then x=y+a
- Option B: If x+a>y+a, then x>y
- Option C: If x<y, then x+a>y+a
- Option D: If x>y, then x+a<y+a
From the options, we can see that option B matches our derived converse statement.
Conclusion
Thus, the correct answer is:
Option B: If x+a>y+a, then x>y.
---
The original statement can be expressed in the form of an implication:
- Let P: x>y
- Let Q: x+a>y+a
The converse of an implication P⟹Q is Q⟹P. Therefore, we need to express the converse:
- The converse will be: "If x+a>y+a, then x>y".
Now we can write the converse statement clearly:
- If x+a>y+a, then x>y.
Now, we need to check which of the given options matches our converse statement:
- Option A: If x<y, then x=y+a
- Option B: If x+a>y+a, then x>y
- Option C: If x<y, then x+a>y+a
- Option D: If x>y, then x+a<y+a
Thus, the correct answer is:
Option B: If x+a>y+a, then x>y.
Topper's Solved these Questions
- MATHEMATICAL REASONINGBOOK - ICSECHAPTER - MATHEMATICAL REASONINGEXERCISE - EXERCISE 27 (a)
16 Videos
- MATHEMATICAL REASONINGBOOK - ICSECHAPTER - MATHEMATICAL REASONINGEXERCISE - EXERCISE 27 (b)
8 Videos
- MATHEMATICAL REASONINGBOOK - ICSECHAPTER - MATHEMATICAL REASONINGEXERCISE - CHAPTER TEST
10 Videos
- MATHEMATICAL INDUCTIONBOOK - ICSECHAPTER - MATHEMATICAL INDUCTIONEXERCISE - Exercise (a)
1 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - EXERCISE
14 Videos
Similar Questions
Knowledge Check
The converse of the statement If you can vote then you are more than 18 years old is
A1. If you are more than 18 year old then you can vote.B2. If you are not more than 18 years old then you cannot vote.C3. If you cannot vote then you are not more than 18 years old.D4. If you are not more than 18 years then you can vote.The converse of the statement If two lines are parallel , then they do not intersect in the plane is
A1. If two lines do not intersect in the same plane then they are parallel.B2. If two lines are not parallel then they do not intersect in the same plane.C3. If two lines are not parallel then they intersect in the same plane.D4. none of the above
The converse of the statement ''If sum is not shining, then sky is filled with clouds '' is
View SolutionThe converse of a given statement "if p, then q" is (where f and q are statements)
View SolutionWhich of the following statement is converse of the statement ''if if rains then we will party''?
View SolutionIn the conversion of
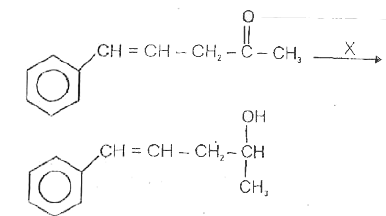
X is
View SolutionWrite the converse, contradiction and contrapositive of the statement 'If x+3=9,then x=6.?
View SolutionWrite the converse of the statement. If a number is divisible by 9, then it is divisible by 3.
View Solution
