The coordinates (2, 3) and (1, 5) are the foci of an ellipse which passes through the origin. Then the equation of the tangent at the origin is (3√2−5)x+(1−2√2)y=0 tangent at the origin is (3√2+5)x+(1+2√2y)=0 tangent at the origin is (3√2+5)x−(2√2+1)y=0 tangent at the origin is (3√2−5)−y(1−2√2)=0
tangent at the origin is (3√2−5)x+(1−2√2)y=0
tangent at the origin is (3√2−5)x+(1+2√2)y=0
tangent at the origin is (3√2−5)x−(2√2+1)y=0
tangent at the origin is (3√2−5)−y−(1−2√2)=0
Tangent and normal are bisector of ∠SPS
Now, the eqaution of SP is y=3x/2 and that of SP is y=5,
Then equation of angle bisectors are
3x−2y√13=±5x−y√26
or 3x−2y=+5x−y√2
Therefore ,the lines are
(3√2−5)x+(1−2√2)y=0
and (3√2+5)x−2√2+1)y=0
Now, (2,3) and (1,5) line on the same side of (3√3−5)x+(1−2√2y=0, which is the equation of tangent.
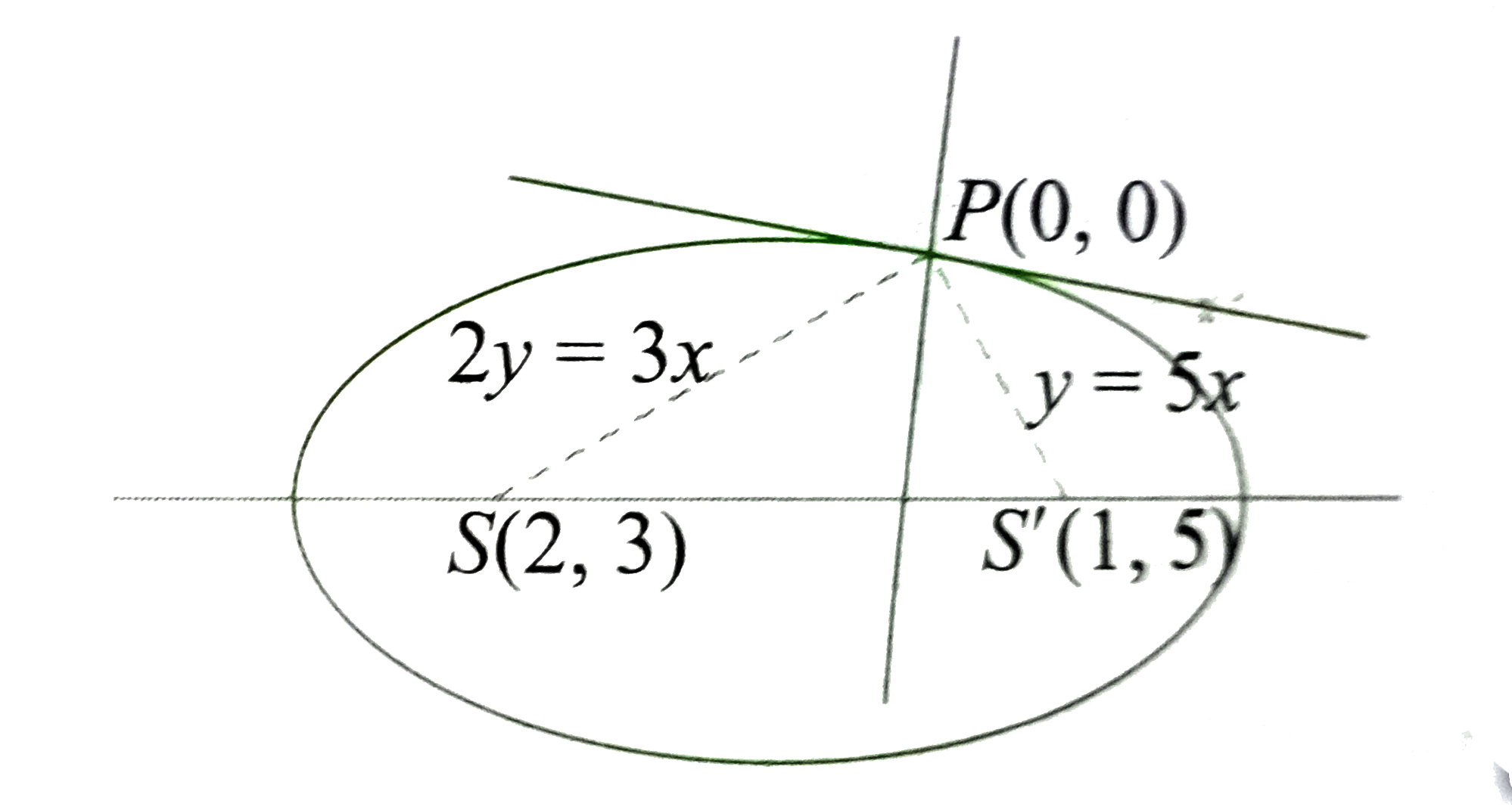
Points (2,3) adn (1,5) a line on the different sides of (3√2+5)x+(2−√2+1)y=0, which is the equation of normal
Similar Questions
The coordinates (2, 3) and (1, 5) are the foci of an ellipse which passes through the origin. Then the equation of the (a)tangent at the origin is (3√2−5)x+(1−2√2)y=0 (b)tangent at the origin is (3√2+5)x+(1+2√2y)=0 (c)tangent at the origin is (3√2+5)x−(2√2+1)y=0 (d)tangent at the origin is (3√2−5)−y(1−2√2)=0
View Solution2√3x2+x−5√3=0
View Solutionx2+(3−√5)x−3√5=0
View SolutionFind the equation of tangent to the curve y=sin−1(2x)1+x2atx=√3
View SolutionFind the equation of the tangent line to the curve y=√5x−3−2 which is parallel to the line 4x−2y+3=0
View SolutionFind the equation of the tangent to the curve y=√3x−2which is parallel to the line 4x−2y+5=0.
View SolutionFind the equation of the tangent to the curve y=√3x−2 which is parallel to the line 4x−2y+5=0.
View SolutionFind the equation of the tangent to the curve y=√3x−2 which is parallel to the line 4x−2y+5=0
View SolutionFind the equation of tangent to y=∫x3x2dt√1+t2atx=1.
View Solution√2x+√3y=0
√5x−√2y=0
View Solution
