The coordinates of the vertices of a triangle are and Prove that the coordinates of its centroid are , . Solution in Odia
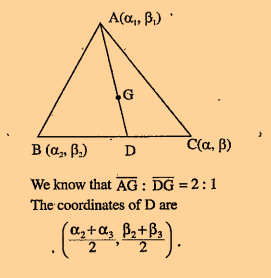
the coordinates of C are
=
which is the centroid of the triangle ABC.
Topper's Solved these Questions
Similar Questions
If the values observed are 1,2,…..,n each with frequency 1, find the mean value
View SolutionThe number of lines making equal angles with coordinate axes is_____.
View SolutionLet log_3^N = alpha_1 + beta_1 , log_5^N = alpha_2 + beta_2 , log_7^N = alpha_3 + beta_3 Largest integral value of N if alpha_1 =5 , alpha_2 = 3 and alpha_3=2(A)342. (D) 242 (C) 243 (B) 343 342 17 Difference of largest and smallest integral values of N if alpha_1 =5 , alpha_2 = 3 and alpha_3=2 (D) 99 (C) 98 (B) 100 (A) 97
View SolutionLet −π6<θ<−π12. Supposeα1 and β1 are two roots of the equation x2−2xsecθ+1=0 and α2 and β2 are the roots of the equation x2−2xtanθ−1=0. If α1>β1 and α2>β2 then α1+β2 equals
View SolutionA : If (2,1,−3),(−2,3,4),(1,2,2) are the midpoints of ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC then A=(−3,4,9)
R : If (α1,β1,γ1),(α2,β2,γ2),(α3,β3,γ3) are the midpoints of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC then A=(α2+α3−α1,β2+β3−β1,γ2+γ3−γ1)
View SolutionLet α1,β1 be the roots x2−6x+p=0and α2,β2 be the roots x2−54x+q=0. If α1,β1,α2,β2 form an increasing G.P., then sum of the digits of the value of (q−p) is ___________.
View SolutionLet α1,β1 be the roots x2−6x+p=0and α2,β2 be the roots x2−54x+q=0. If α1,β1,α2,β2 form an increasing G.P., then sum of the digits of the value of (q−p) is ___________.
View SolutionIf cos(α1−α2)cos(α1+α2)=cos(α3+α4)cos(α3−α4)=0 then tanα1⋅tanα2⋅tanα3⋅tanα4 =............
View SolutionIf (α1,β1),(α2,β2),(α3,β3)and(α4,β4) are the vertices of a parallelogram,show that α1+α3=α2+α4 and β1+β3=β2+β4.
View SolutionLet −π6<θ<−π12. Suppose α1andβ1, are the roots of the equation x2−2xsecθ+1=0 and α2andβ2 are the roots of the equation x2+2xtanθ−1=0. If α1>β1 and α2>β2, then α1+β2 equals:
View SolutionLet t be the trace of matrix A[(|x+y||x|+|y|,α1,β1),(α2,|y+z||y|+|z|,β2),(α3,β3,(|z+x||z|+|x|)] then
View SolutionLet logN3=α1+β1,logN5=α2+β2,logN7=α3+β3 Largest integral value of N if α1=5,α2=3andα3=2andβ1,β2,β3=(0,1)(A)342. (D) 242 (C) 243 (B) 343 342 17 Difference of largest and smallest integral values of N if α1=5,α2=3andα3=2andβ1,β2,β3=(0,1) (D) 99 (C) 98 (B) 100 (A) 97
View SolutionIf √α1−1+2√α2−4+3√α3−9+4√α4−16=α1+α2+α3+α42whereα1,α2,α3,α4 are all real. Thena. α1+α2=10 b. α2+α3=26 c. α4−α3=12 d. α4−α2−α1=22
View SolutionLet α1,β1 be the roots x2−6x+p=0and α2,β2 be the roots x2−54x+q=0. If α1,β1,α2,β2 form an increasing G.P., then sum of the digits of the value of (q−p) is ___________.
View SolutionLet −16<θ<−π12 Suppose α1andβ1, are the roots of the equation x2−2xsecθ+1=0 and α2andβ2 are the roots of the equation x2+2xtanθ−1=0. If α1>β1 and α2>β2, then α1+β2 equals
View Solution
