The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
p = q
p=2q
q=2p
q=3p
The correct Answer is:D
Step by step video & text solution for The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q gt 0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - EXERCISE 12 (C ) (B.Fill in the Blanks)
5 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - EXERCISE 12 (C ) (True/False Questions)
5 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - EXERCISE 12 C (Long Answer Type Questions )
23 Videos
- INVERSE - TRIGONOMETRIC FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - INVERSE - TRIGONOMETRIC FUNCTIONSEXERCISE - CHAPTER TEST (2)
11 Videos
- MATRICESBOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)
12 Videos
Similar Questions
The corner points of the feasible region determined by the following system of linear inequalities:
2x+y≥10,x+3y≤15,x,y≥0 are (0,0),(5,0),(3,4) and (0,5). Let Z=px+qy, where p,q≥0. Condition on p and q so that the maximum of Z occurs at both (3,4) and (0,5) is:
(a) p=q (b) p=2q (c) p=eq (d) q=3p
View SolutionFor an objective function Z=ax+by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
View Solution
Knowledge Check
The corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
A5p = 2qB2p=5qCp = 2qDq = 3pCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1), and (3,0). Let Z=px+qy. Where p,q<0 Condition on p and q, so that the minimum of Z occurs at (3,0) and (1,1) is
Ap=2qBp=q2Cp=3qDp=qFor an objective function Z = ax + by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20). (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum z occurs at both the points (30, 30) and (0, 40) is:
Ab−3a=0Ba=3bCa+2b=0D2a−b=0
The corner points of the feasible region determined by the system of linear constraints are as shown below:
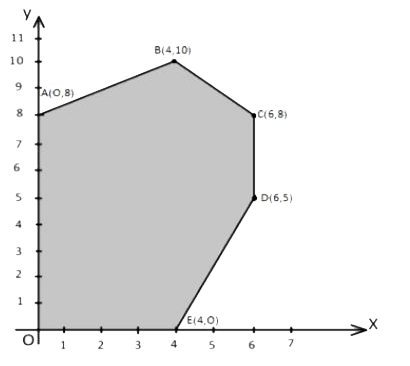
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.
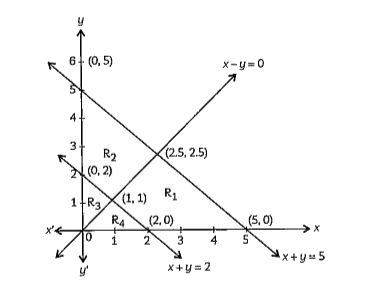
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
View SolutionThe corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
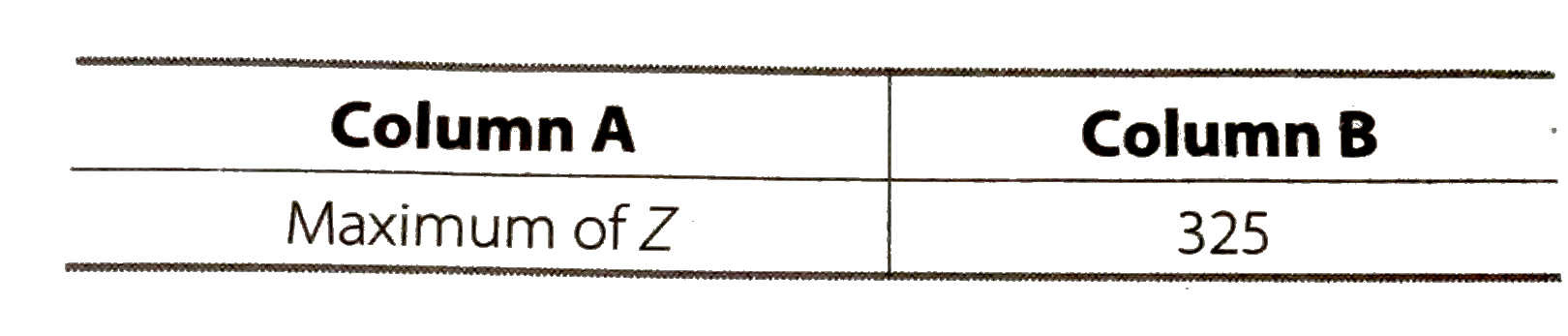
View SolutionThe corner points of the feasible region of a system of linear inequations are (0, 0), (5, 0), (6,5), (6, 8), (4, 10) and (0,8). If Z = 3x - 4y, then the minimum value of Z occurs at:
View Solution
