The data on the number of patient attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.
Take the assumed mean as 45. Give your answer correct to 2 decimal places.

The correct Answer is:40.33
Step by step video & image solution for The data on the number of patient attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method. Take the assumed mean as 45. Give your answer correct to 2 decimal places. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The data on the number of patients attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.

View SolutionThe following table shows the ages of the patients admitted in a hospital during a year:Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
View SolutionThe given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the
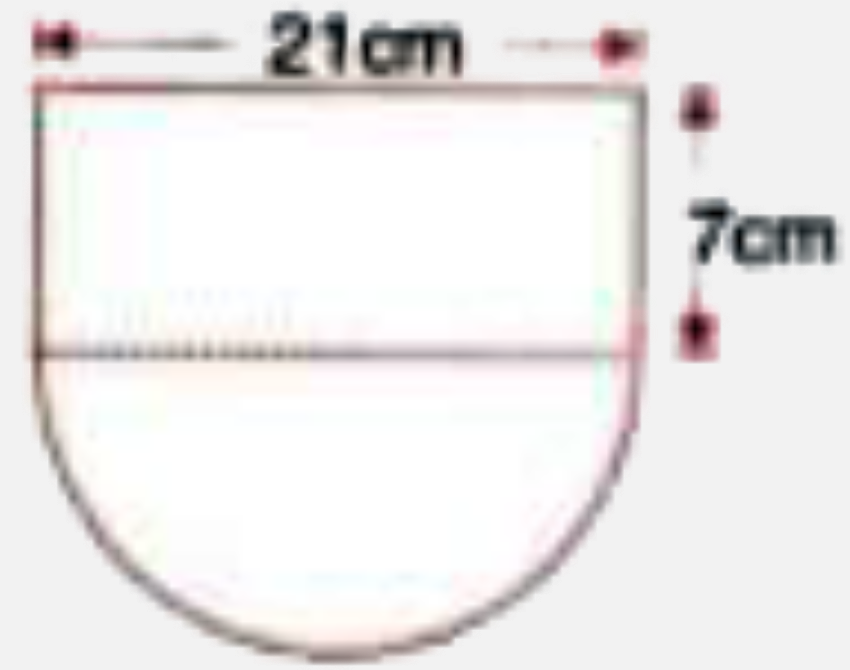
volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
View SolutionA solid consisting of a right circular cone, standing on a hemisphere, is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm, the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer correct to the nearest centimetre
( Take π=317)
View SolutionConsider the compound given below

Find x+y+z where
x=total number of optically active isomers
y=total number of optically inactive isomers
z=total number of alternating axis of symmetry in its steroisomers
Fill your answer as sum of digits (excluding decimal places) till you get the single digit answer.
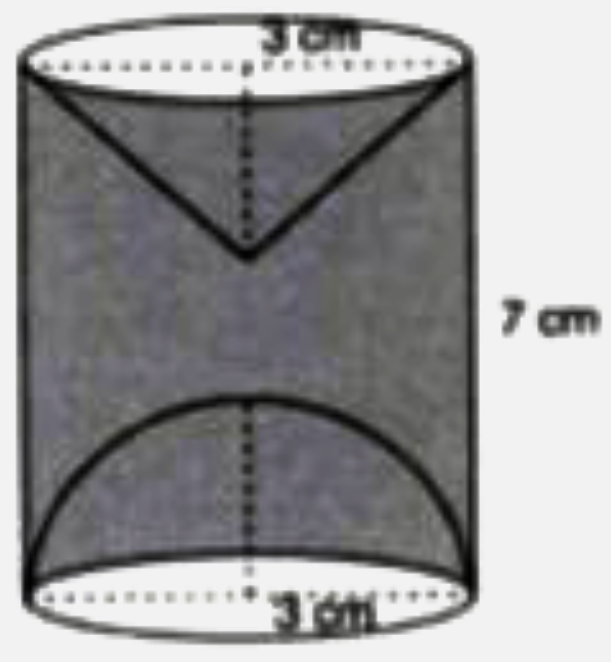
View SolutionA hemispherical and a conical hole are scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as as given alongside :
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number. Take π=227.
View SolutionThe following table shows the ages of the patients admitted in a hospital during a year: Age (in years): 5-15 15-25 25-35 35-45 45-55 55-65 No. of students: 6 11 21 23 14 5 Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
View SolutionA survey was conducted by a group of students as a part of their environment awareness programme , in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house. Number of plants: 0-2 2-4 4-6 6-8 8-10 10-12 12-14 Number of houses: 1 2 1 5 6 2 3 Which method did you use for finding the mean, and why?
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
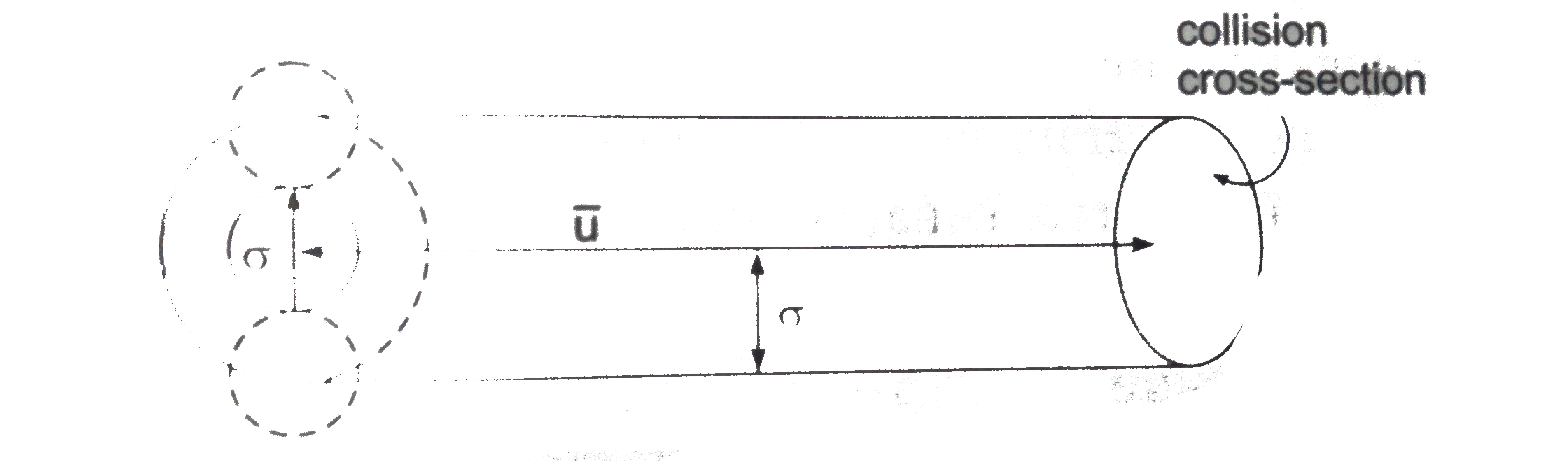
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
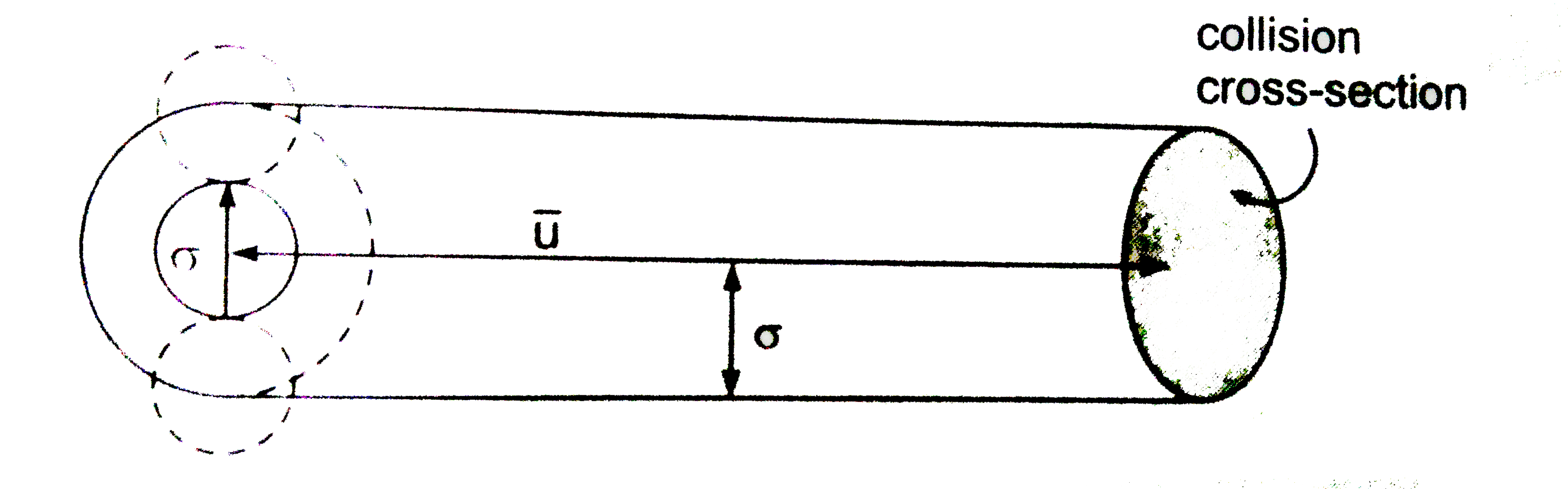
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.
View Solution
