The demand function for a certain item is given by p = 5000 - 200x. What will be the total revenue from the sale of 5 units?
20000
25000
15000
10000
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
Knowledge Check
The demand function of a monopolist is given by x = 100 - 4p. The quantity at which MR (marginal revenue) = 0 will be
A25B10C50D40The given table represents the revenue (in ₹ crores) of a company from the sale of four products A,B,C and D in 6 years. Study the table carefully and answer the questions that follow.
दी गयी तालिका एक कंपनी को चार उत्पादों -A, B, C तथा D की बिक्री से 6 वर्षों में होने वाली आय ( करोड़ रुपये में ) को दर्शाती है | इस तालिका का ध्यानपूर्वक अध्ययन करें तथा फिर पूछे गए प्रश्नों का उत्तर दें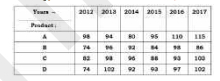
The total revenue of the company from the sale of products B,C and D in 2014 is what percentage of
the total revenue from the sale of products C and D in 6 years?
2014 में उत्पाद B, C और D की बिक्री से कंपनी को हुई कुल आय 6 वर्षों में उत्पाद C और D की बिक्री से हुई कुल आय का कितना प्रतिशत है?A18B20C25D28
The demand function of a certain commodity is given by p=1000−25x+x2 where 0≤x≤20 . Find the price per unit and total revenue from the sale of 5 units.
View SolutionThe demand function for a certain product is represented by p = 200 + 20 x - x2 (in rupees). Obtain the marginal revenue when 10 units are sold.
View SolutionThe demand for a certain product is represented by the equation p=500+25x−x23 in rupees where is the number of units and p is the price per unit Find :
(i) Marginal revenue function.
(ii) The marginal revenue when 10 units are sold.
View SolutionA monopolist's demand function is p= 300 - 5x. At what price is the marginal revenue zero.
View SolutionIf the marginal revenue (MR) function is defined as the rate of change of total revenue (R ) with respect to the quantity demanded at an instant. IF the marginal revenue of a function is given by:
MR=25e−x/400(1−x100)
find the total revenue function through integration, putting the condition that R=6 when x=0
View SolutionThe revenue function is given by R(x)=100x−x2−x3 . Find
(i) The demand function.
(ii) Marginal revenue function.
View Solution