The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
GIVEN A quadrilateral ABCD whose diagonals AC and BD intersects at a point O such that
AOOC=BOOD
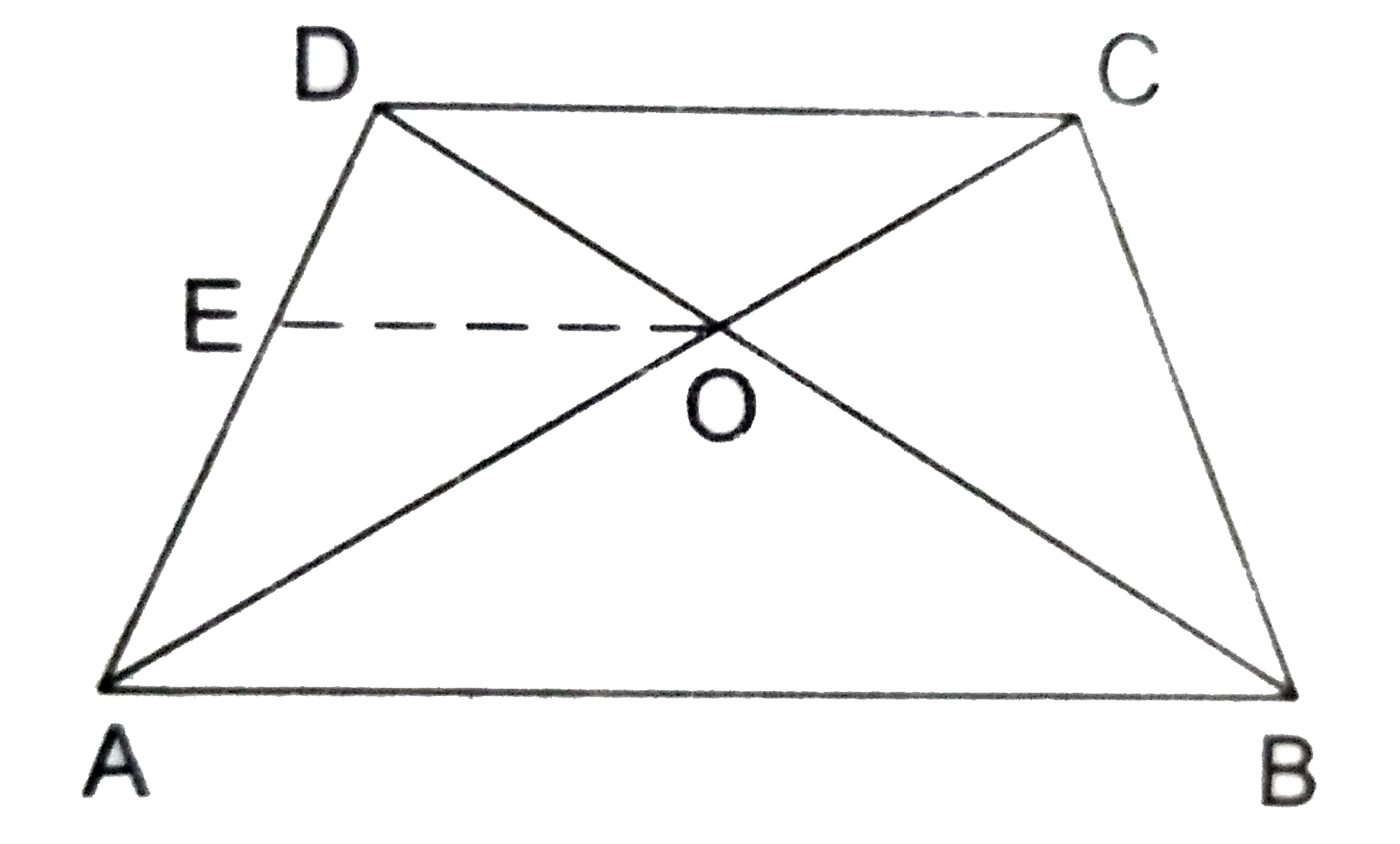
TO PROVE ABCD is a trapezium, i.e., AB∣∣DC.
CONSTRUCTION Draw EO∣∣DC, meeting AD at E.
PROOF In ΔACD,EO∣∣DC.
∴AOOC=AEED [ by Thale's theorme]
But ,AOOC=BOOD (give)
∴BOOD=AEED⇒DOOB=DEEA inΔAB.
So, EO∣∣AB [ by the converse of Thale's theorem]
But, EO∣∣DC
Hence, AB∣∣DC,i.e.,ABCD is a trapezium.
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionThe diagonal of a quadrilateral ABCD intersect each other at the point D such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View SolutionThe diagonals of a rectangle ABCD intersects at O. If ∠BOC=70∘. find ∠ODA.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other as the point O. Show that AOBO=CODO.
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solution
