The diagonals of a rhombus are 18 cm and 24 cm. Find ,
(i) its area (ii) length of its sides (iii) its perimeter
The correct Answer is:(i) 216cm2 (ii) 15 cm (iii) 60 cm
To solve the problem step by step, we will find the area, length of the sides, and perimeter of the rhombus given its diagonals.
Step 1: Find the Area of the Rhombus
The formula for the area of a rhombus when the lengths of the diagonals are known is:
Area=12×d1×d2
where d1 and d2 are the lengths of the diagonals.
Given:
- d1=24cm
- d2=18cm
Substituting the values into the formula:
Area=12×24×18
Calculating the area:
Area=12×432=216cm2
Step 2: Find the Length of the Sides of the Rhombus
The diagonals of a rhombus bisect each other at right angles. Therefore, we can use the right triangle formed by half of each diagonal to find the length of a side.
Let O be the intersection point of the diagonals. Then:
- OA=d12=242=12cm
- OB=d22=182=9cm
Using the Pythagorean theorem in triangle AOB:
AB2=OA2+OB2
Substituting the values:
AB2=122+92
Calculating:
AB2=144+81=225
Taking the square root to find AB:
AB=√225=15cm
Step 3: Find the Perimeter of the Rhombus
The perimeter P of a rhombus is given by:
P=4×side
Since all sides are equal and we found AB=15cm:
P=4×15=60cm
Summary of Results
(i) Area of the rhombus: 216cm2
(ii) Length of each side: 15cm
(iii) Perimeter of the rhombus: 60cm
---
The formula for the area of a rhombus when the lengths of the diagonals are known is:
- d1=24cm
- d2=18cm
The diagonals of a rhombus bisect each other at right angles. Therefore, we can use the right triangle formed by half of each diagonal to find the length of a side.
- OB=d22=182=9cm
The perimeter P of a rhombus is given by:
(i) Area of the rhombus: 216cm2
(ii) Length of each side: 15cm
(iii) Perimeter of the rhombus: 60cm
Topper's Solved these Questions
- AREA OF A TRAPEZIUM AND A POLYGONBOOK - ICSECHAPTER - AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - EXERCISE 20(D)
21 Videos
- AREA OF A TRAPEZIUM AND A POLYGONBOOK - ICSECHAPTER - AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - EXERCISE 20(B)
19 Videos
- ALGEBRAIC EXPRESSIONS BOOK - ICSECHAPTER - ALGEBRAIC EXPRESSIONS EXERCISE - Exercise 11(E)
15 Videos
- CONSTRUCTION (USING RULER AND COMPASSES ONLY)BOOK - ICSECHAPTER - CONSTRUCTION (USING RULER AND COMPASSES ONLY)EXERCISE - EXERCISE 18(D)
10 Videos
Similar Questions
The diagonals of a rhombus are 16 cm and 12 cm, find:
(i) its area (ii) length of its side (iii) its perimeter.
View SolutionThe diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
View SolutionThe diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
View SolutionThe diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter
View SolutionThe diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter
View SolutionThe diagonals of a rhombus are 24 cm and 10 cm. Calculate its area and perimeter.
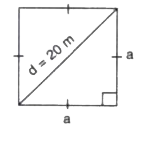
View SolutionThe diagonal of a square is 20m. Find its:
(i) area (ii) length of one side (iii) perimeter
View SolutionThe lengths of the diagonals of a rhombus are 12 cm and 16 cm. Find the area of rhombus
View SolutionIf the diagonals of a rhombus are 12cm and 16cm, find the length of each side.
View SolutionIf the diagonals of a rhombus are 12cm and 16cm, find the length of each side.
View Solution
