The diameter of a coin is 1 cm (Fig. 15.83). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π=3.1416) (FIGURE)
Step by step video & image solution for The diameter of a coin is 1 cm (Fig. 15.83). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (T a k e\ pi=3. 1416) (FIGURE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
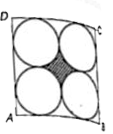
ABCD is a square , inside which 4 circles with radius 1 cm , each are touching each other . What is the area of the shaded region ?
 A(2π−3)cm2B(4−π)cm2C(16−4π)cm2Dnone of these
A(2π−3)cm2B(4−π)cm2C(16−4π)cm2Dnone of theseThree coins of the same size (radius 1 cm) are placed on a table such that each of them touches the other two. The area enclosed by the coins is
A(a) (π2−√3)cm2B(b) (√3−π2)cm2C(c) (2√3−π2)cm2D(d) (3√3−π2)cm2Three coins of the same size (radius 1 cm) are placed on a table such that each of them touches the other two. The area enclosed by the coins is
A(π2−√3)cm2B(√3−π2)cm2C(2√3−π2)cm2D(3√3−π2)cm2
Four equal circles are described about the four corners of a square so that each touches two of the others as shown in Fig. 15.38. Find the area of the shaded region, each side of the square measuring 14 cm. (FIGURE)
View SolutionIn the figure, ΔABC is in the semi-circle, find the area of the shaded region given that AB = BC = 4 cm. (use π=3.14 )

View SolutionIn Fig. 15.77, PQRS is a square of side 4 cm. Find the area of the shaded region. (FIGURE)
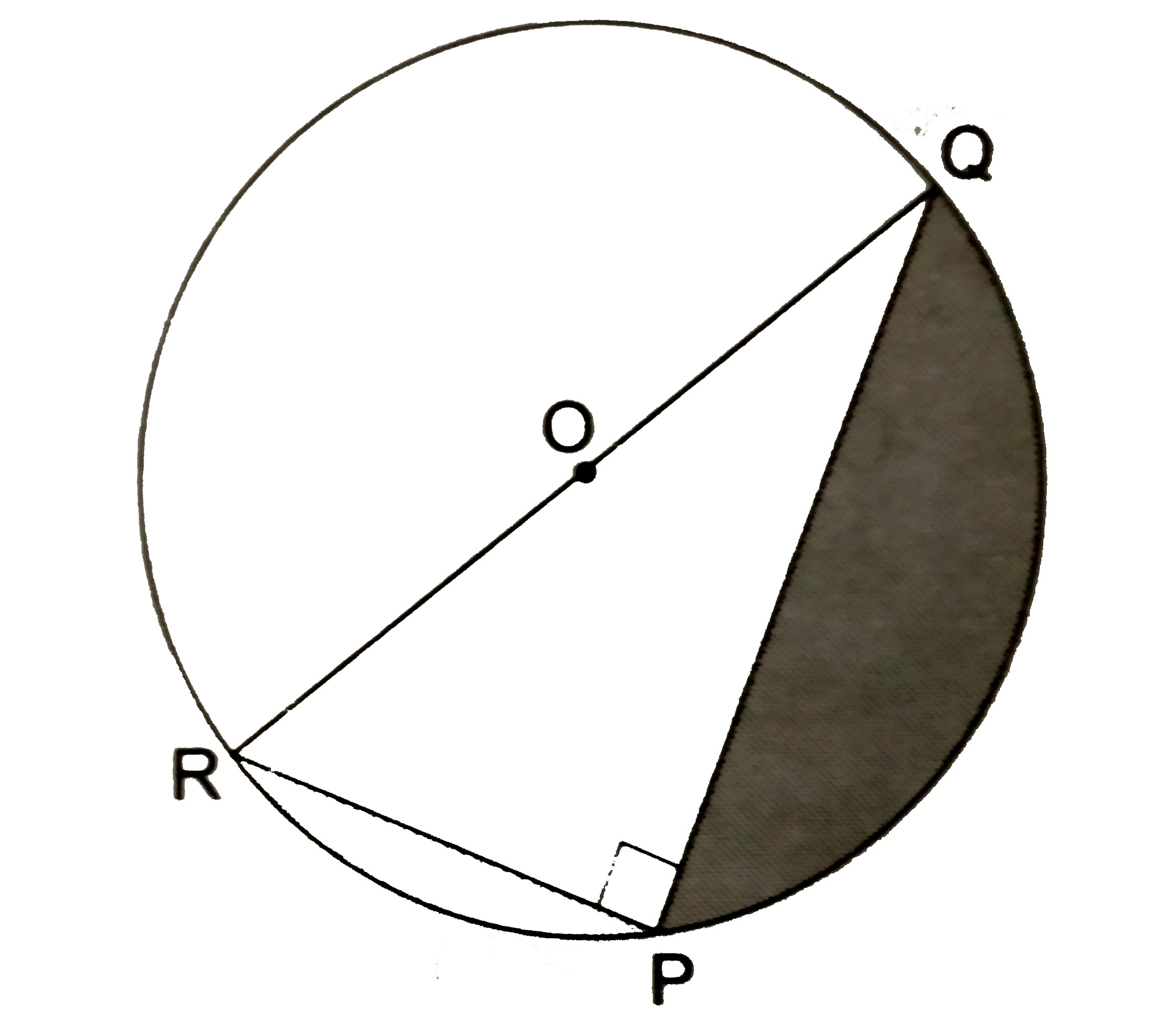
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)

View SolutionABCD is a square of 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region. (π=3.14)
View Solution