The distance between two poles of the same height standing on the same plane is 100m.The angles of elevation of the tops of the two poles from a point lying on the line joining the base-points of the poles are found to be 30∘and 60∘respectively.Find the heights of the poles and the position of the point.Solution in Assamese
Step by step video & image solution for The distance between two poles of the same height standing on the same plane is 100m.The angles of elevation of the tops of the two poles from a point lying on the line joining the base-points of the poles are found to be 30^@and 60^@respectively.Find the heights of the poles and the position of the point. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
A circus artist is climbing a 20 m long rope.which is tightly stretched and tied from the top of a vertical pole to the ground.Find the height of the pole,if the angle made by the rope with the ground level is 30∘(see Fig 9.11)
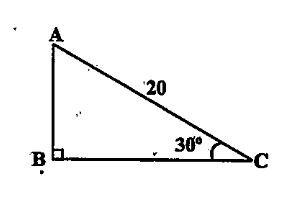 03:41View Solution
03:41View SolutionWhich of the following ratios are in proportion? 12 : 21 and 32 : 56
03:50View SolutionWhat is the median of the data 15,8,10,6,12,11,4,7,3?
06:42View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
03:53View Solutionदो ऊर्ध्वाधर खम्भों के बीच कि दूरी 100m है और एक कि ऊँचाई दूसरे कि दुगुनी है। दोनों खम्भों के पादो को मिलाने वाली रेखा पर के किसी बिंदु पर खम्भों के शिखरों के उन्नयन कोण 30∘ और 60∘ है उनकी ऊँचाइयाँ ज्ञात कीजिये।
View SolutionTwo poles of equal height are standing opposite to each other on either sidef of the road, which is 120 feet wide. From a point between then on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
04:15View SolutionTwo poles of equal height are standing opposite to each other on either side of the road, which is 80 m wide. From a point between then on the road, the angles of elevation of top of the poles are 60∘ and 30∘. Find the height of poles.
04:45View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ to 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
05:12View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
04:41View SolutionFrom the top of a tower 50 m high, the angle of depression of the top of a pole is 45∘ and from the foot of the pole, the angle of elevation of the top of the tower is 60∘. Find the height of the pole if the pole and tower stand on the same plane.
06:09View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.
02:46View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
03:49View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.
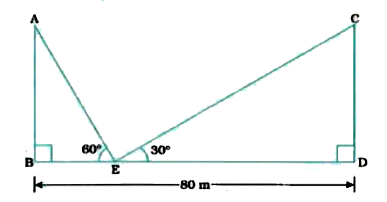 04:25View Solution
04:25View SolutionA pole stands erect on the ground. If the angle of elevation of the top of the pole from a point 90m away from the foot of the pole is 30∘, find the height of the pole.
08:21View SolutionThe angle of elevation of an electric pole from a point A on the ground is 60∘ and from a Point B towards the pole on the line joining the foot of the pole to the point A, is 75∘. If the distance AB = a, then the height of the pole is
06:09View Solution

