The distance of the point (1,2) from the line 2x−3y−4=0 in the direction of the line x+y=1 , is
√2
5√2
1√2
none of these
The correct Answer is:A
The equation of a line passing through P(1,1) and parallel to x+y=1, is
x−1cos3π4=y−1sin3π4
Let PM=r. Then , the coordinates of M are given by
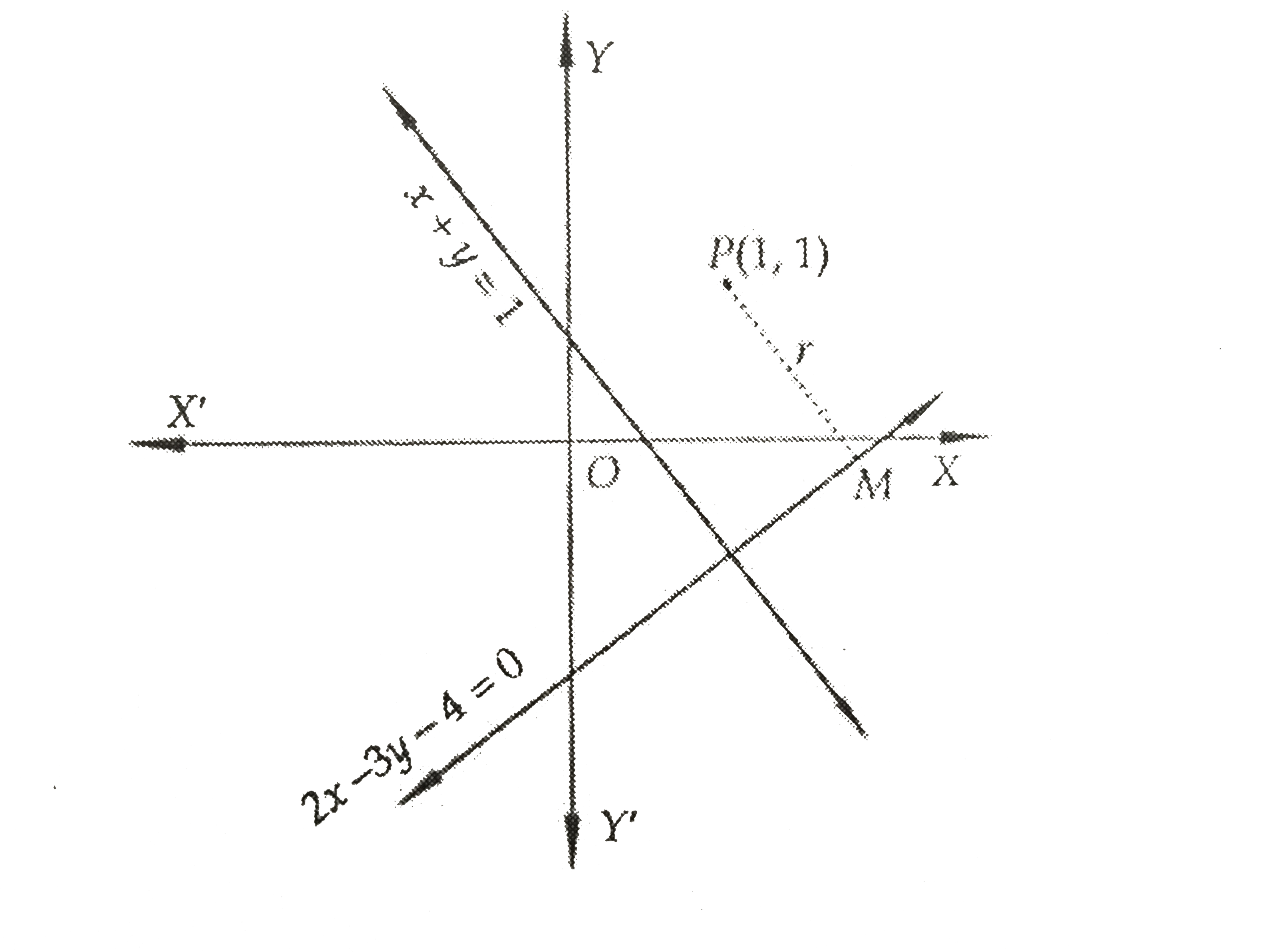
x−1cos(3π)4=y−1sin(3π)4=r or , (1−r√2,1+r√2)
∵ M lies on 2x−3y−4=0
∴2(1−r√2)−3(1+r√2)−4=0
⇒2−2r√2−3−3r√2−4=0⇒−5−5r√2=0⇒r=−√2
Hence , PM =√2
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section I - Solved Mcqs
64 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
The distance of the point (-2,6) from the line 3x−4y− 10=0
View SolutionThe distance of the point (3,0,5) from the line x−2y+2z−4=0=x+3z−11 is
View SolutionDistance of point (1,3) from the line 2x−3y+9=0 along x−y+1=0
View SolutionFind the distance of the line 2x+y=3 from the point(−1, −3) in the direction of the line whose slope is 1.
View SolutionFind the distance of the point (2,3) from the line 2x−3y+9=0 measured along a line x−y+1=0.
View SolutionFind the distance of the point (2,3) from the line 2x−3y+9=0 measured along the line 2x−2y+5=0
View SolutionFind the distance of the point (3,5) from the line 2x+3y=14 measured parallel to the line x−2y=1.
View SolutionFind the distance of the point (−1,−5,−10) from the point of intersection of the line x−23=y+14=z−212 and plane x−y+z=5.
View SolutionFind the distance of the point (−1,−5,−10) from the point of intersection of the line x−23=y+14=z−212 and plane x−y+z=5.
View SolutionFind the distance of the point (2,5) from the line 3x+y+4=0 measured parallel to the line 3x−4y+8=0
View Solution
