The distance of two points P and Q on the parabola $y^{2} = 4 a x$ from the focus S are 3 and 12 respectively. The distance of the point of intersection of the tangents at P and Q from the focus S is

A

8

B

6

C

9

D

12

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

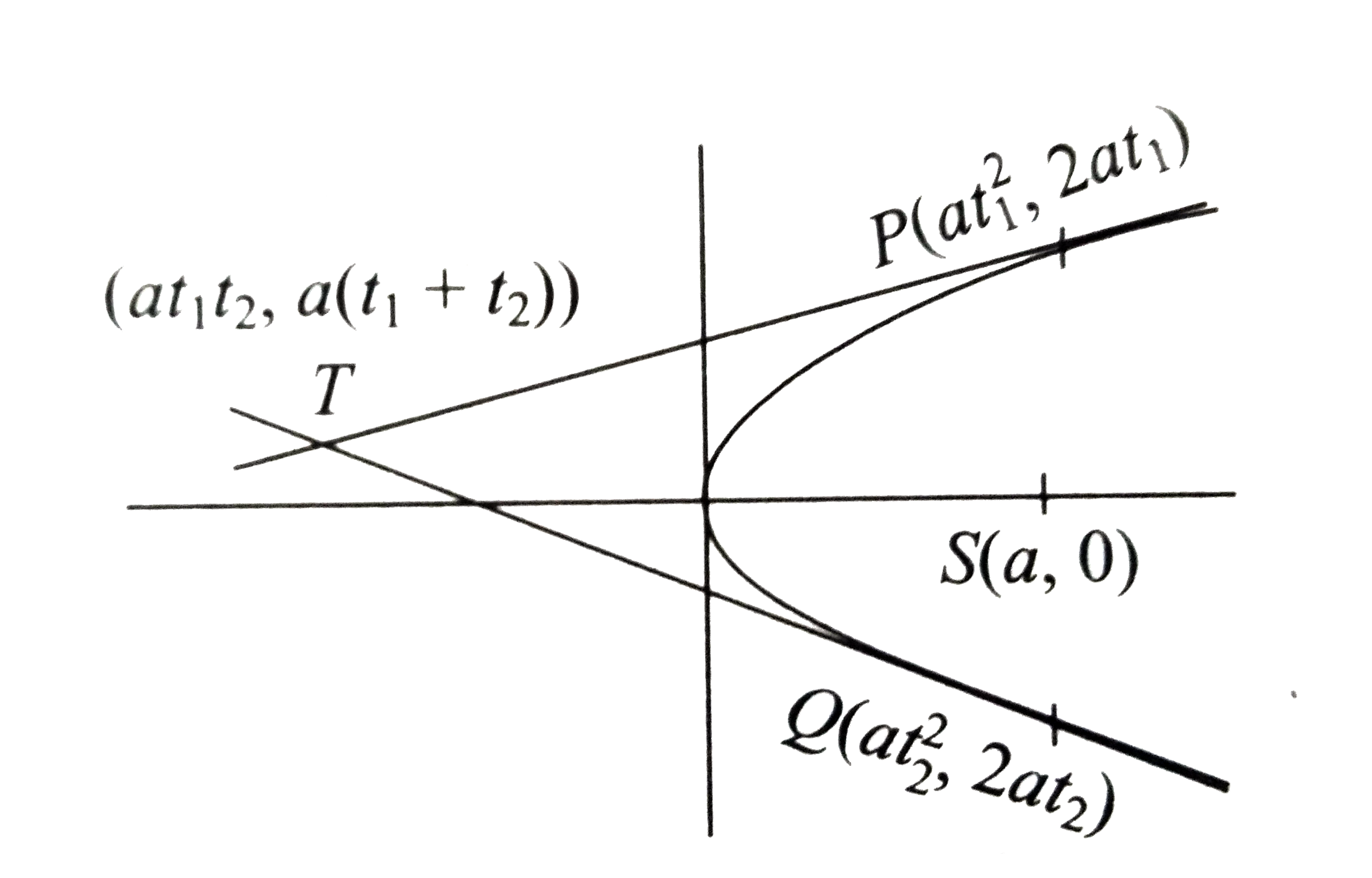
If $P (a t_{1}^{2}, 2 a t_{1})$ and $Q (a t_{2}^{2}, 2 a t_{2})$ , and $T (a t_{1} t_{2}, a (t_{1} + t_{2}))$
Thus, we have $S T^{2} = S P \times S Q = 3 \times 12 = 36$
$∴ S T = 6$

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The line $4 x - 7 y + 10 = 0$ intersects the parabola $y^{2} = 4 x$ at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
A $(- \frac{7}{2}, - \frac{5}{2})$
B $(\frac{5}{2}, \frac{7}{2})$
C $(- \frac{5}{2}, - \frac{7}{2})$
D $(\frac{7}{2}, \frac{5}{2})$
Question 2 - Select One
Distance of a point P on the parabola $y^{2} = 48 x$ from the focus is l and its distance from the tangent at the vertex is d then l-d is equal to
A4
B8
C12
D16
Question 3 - Select One
If $y_{1}, y_{2}$ are the ordinates of two points P and Q on the parabola and $y_{3}$ is the ordinate of the intersection of tangents at P and Q, then
A $y_{1}, y_{2}, y_{3}$ are in A.P.
B $y_{1}, y_{3}, y_{2}$ are in A.P.
C $y_{1}, y_{2}, y_{3}$ are in G.P
D $y_{1}, y_{3}, y_{2}$ are in G.P.

CENGAGE-PARABOLA-Single Correct Answer Type

Home
Ask Doubt
Profile