The distribution below gives the weight of 30 students in a class. Find the median weight of students: Weight (in kg): 40-45 45-50 50-55 55-60 60-65 65-70 70-75 No. of students: 2 3 8 6 6 3 2
To find the median weight of the students given the distribution, we will follow these steps:
Step 1: Organize the Data
We have the following data:
| Weight (in kg) | Number of Students |
|----------------|--------------------|
| 40 - 45 | 2 |
| 45 - 50 | 3 |
| 50 - 55 | 8 |
| 55 - 60 | 6 |
| 60 - 65 | 6 |
| 65 - 70 | 3 |
| 70 - 75 | 2 |
Step 2: Calculate the Total Number of Students
Add the number of students in each weight class to find the total number of students (n).
n=2+3+8+6+6+3+2=30
Step 3: Calculate the Cumulative Frequency
Now, we will calculate the cumulative frequency (CF):
| Weight (in kg) | Number of Students | Cumulative Frequency |
|----------------|--------------------|----------------------|
| 40 - 45 | 2 | 2 |
| 45 - 50 | 3 | 5 |
| 50 - 55 | 8 | 13 |
| 55 - 60 | 6 | 19 |
| 60 - 65 | 6 | 25 |
| 65 - 70 | 3 | 28 |
| 70 - 75 | 2 | 30 |
Step 4: Identify the Median Class
To find the median, we need to determine the median class. The median position is given by n2.
n2=302=15
Now, we look for the cumulative frequency that is greater than or equal to 15. The cumulative frequency just exceeding 15 is 19, which corresponds to the weight class 55 - 60. Thus, the median class is 55 - 60.
Step 5: Identify the Values Needed for the Median Formula
- l (lower boundary of median class) = 55
- f (frequency of median class) = 6
- CF (cumulative frequency of the preceding class) = 13
- h (class width) = 5 (since 60 - 55 = 5)
Step 6: Apply the Median Formula
The formula for the median in a grouped frequency distribution is:
Median=l+(n2−CFf)×h
Substituting the values we have:
Median=55+(15−136)×5
Calculating the values:
Median=55+(26)×5
Median=55+(13)×5
Median=55+53
Median=55+1.67≈56.67
Final Answer
The median weight of the students is approximately 56.67 kg.
---
We have the following data:
|----------------|--------------------|
| 40 - 45 | 2 |
| 45 - 50 | 3 |
| 50 - 55 | 8 |
| 55 - 60 | 6 |
| 60 - 65 | 6 |
| 65 - 70 | 3 |
| 70 - 75 | 2 |
Add the number of students in each weight class to find the total number of students (n).
Now, we will calculate the cumulative frequency (CF):
|----------------|--------------------|----------------------|
| 40 - 45 | 2 | 2 |
| 45 - 50 | 3 | 5 |
| 50 - 55 | 8 | 13 |
| 55 - 60 | 6 | 19 |
| 60 - 65 | 6 | 25 |
| 65 - 70 | 3 | 28 |
| 70 - 75 | 2 | 30 |
To find the median, we need to determine the median class. The median position is given by n2.
- l (lower boundary of median class) = 55
- f (frequency of median class) = 6
- CF (cumulative frequency of the preceding class) = 13
- h (class width) = 5 (since 60 - 55 = 5)
The formula for the median in a grouped frequency distribution is:
The median weight of the students is approximately 56.67 kg.
Topper's Solved these Questions
Similar Questions
Find the median weight for following Data weight in kg 45,46,48,50,52,54,55
View SolutionFind the mean of the frequency distribution:
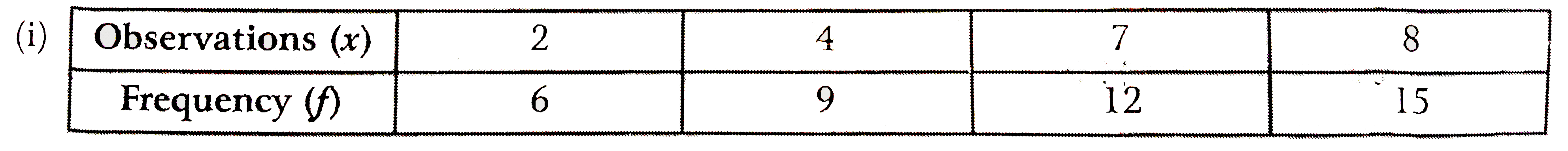
(ii) The weight of 40 students of class IX are given below:
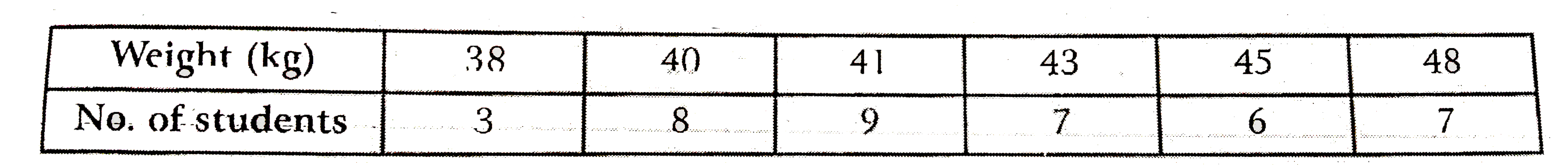 View Solution
View SolutionThe weight (in kg) of students of a class are: Find the mode and median of this data. Is there more than one mode?
View SolutionFollowing table shows the weights of 12 students: Weight (in kgs): 67 70 72 73 75 No. of Students: 4 3 2 2 1 Find the mean weight.
View SolutionFollowing table shows the weights of 12 students:
Weight (in kgs): 67 70 72 73 75
No. of Students: 4 3 2 2 1
Find the mean weight.View SolutionThe mean weight of 60 students in a class is 40 kg. The mean weight of boys is 50 kg while that of girls is 30 kg. Find the number of boys and girls in the class.
View SolutionFind the mean deviation about the mean for the following data: Marks obtained 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Number of students 2 3 8 14 8 3 2
View SolutionCalculate the median from the following data: Rent (in Rs.): 15-25 25-35 35-45 45-55 55-65 65-75 75-85 85-95 No. of Houses: 8 10 15 25 40 20 15 7
View SolutionThe following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate. Literacy rate (in %): 45-55 55-65 65-75 75-85 85-95 Number of cities: 3 10 11 8 3
View SolutionThe following is the distribution of weights (in kg) of 50 persons: Weight (in kg) 50-55 55-60 60-65 65-70 70-75 75-80 80-85 85-90 No. of Person 12 8 5 4 5 7 6 3 Draw a histogram for the above data.
View Solution

