The domain of a function is the set of positive integers less than 12. If y=f(x)=|x−4|, find all ordered pairs satisfying the function. Graph the function.
The correct Answer is:{(1,3),(2,2),(3,1)(4,0),(5,1),(6,2),(7,3),(8,4),(9,5),(10,6),(11,7)} Graph consists of points corresponding to these ordered pairs
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the Domain
The domain of the function is given as the set of positive integers less than 12. Therefore, the domain is:
Domain={1,2,3,4,5,6,7,8,9,10,11}
Step 2: Define the Function
The function is defined as:
y=f(x)=|x−4|
Step 3: Calculate the Function Values
We will calculate the value of f(x) for each integer in the domain.
- For x=1:
f(1)=|1−4|=|−3|=3
- For x=2:
f(2)=|2−4|=|−2|=2
- For x=3:
f(3)=|3−4|=|−1|=1
- For x=4:
f(4)=|4−4|=|0|=0
- For x=5:
f(5)=|5−4|=|1|=1
- For x=6:
f(6)=|6−4|=|2|=2
- For x=7:
f(7)=|7−4|=|3|=3
- For x=8:
f(8)=|8−4|=|4|=4
- For x=9:
f(9)=|9−4|=|5|=5
- For x=10:
f(10)=|10−4|=|6|=6
- For x=11:
f(11)=|11−4|=|7|=7
Step 4: List the Ordered Pairs
Now we can list the ordered pairs (x,f(x)):
- (1,3)
- (2,2)
- (3,1)
- (4,0)
- (5,1)
- (6,2)
- (7,3)
- (8,4)
- (9,5)
- (10,6)
- (11,7)
Step 5: Graph the Function
To graph the function, plot the points from the ordered pairs on a Cartesian plane. The x-axis will represent the values of x (from 1 to 11), and the y-axis will represent the values of f(x).
Summary of Results
The ordered pairs satisfying the function are:
(1,3),(2,2),(3,1),(4,0),(5,1),(6,2),(7,3),(8,4),(9,5),(10,6),(11,7)
The domain of the function is given as the set of positive integers less than 12. Therefore, the domain is:
Domain={1,2,3,4,5,6,7,8,9,10,11}
The function is defined as:
y=f(x)=|x−4|
We will calculate the value of f(x) for each integer in the domain.
f(1)=|1−4|=|−3|=3
- For x=2:
f(2)=|2−4|=|−2|=2
- For x=3:
f(3)=|3−4|=|−1|=1
- For x=4:
f(4)=|4−4|=|0|=0
- For x=5:
f(5)=|5−4|=|1|=1
- For x=6:
f(6)=|6−4|=|2|=2
- For x=7:
f(7)=|7−4|=|3|=3
- For x=8:
f(8)=|8−4|=|4|=4
- For x=9:
f(9)=|9−4|=|5|=5
- For x=10:
f(10)=|10−4|=|6|=6
- For x=11:
f(11)=|11−4|=|7|=7
Now we can list the ordered pairs (x,f(x)):
- (1,3)
- (2,2)
- (3,1)
- (4,0)
- (5,1)
- (6,2)
- (7,3)
- (8,4)
- (9,5)
- (10,6)
- (11,7)
To graph the function, plot the points from the ordered pairs on a Cartesian plane. The x-axis will represent the values of x (from 1 to 11), and the y-axis will represent the values of f(x).
The ordered pairs satisfying the function are:
(1,3),(2,2),(3,1),(4,0),(5,1),(6,2),(7,3),(8,4),(9,5),(10,6),(11,7)
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (d)
18 Videos
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (e)
13 Videos
- RELATIONS AND FUNCTIONSBOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (b)
26 Videos
- RELATION AND FUNCTIONSBOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
32 Videos
- SAMPLE QUESTION PAPER 01BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 01EXERCISE - SECTION C
8 Videos
Similar Questions
Knowledge Check
The range of the polynomial function f is the set of real numbers less than or equal to 4. If the zeros of f are −3 and 1, which of the following could be the graph of y = f (x) in the xy-plane?
A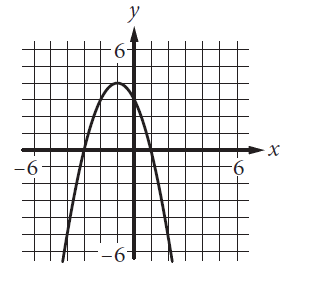 B
B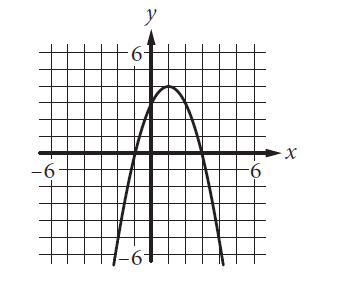 C
C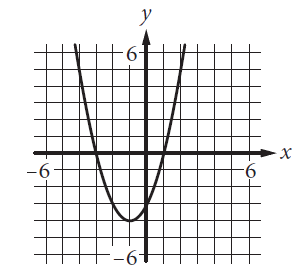 D
D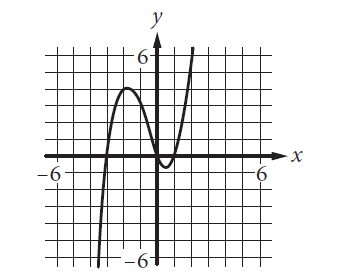
Find the domain of the function log∣∣4−x2∣∣.
View SolutionFind the domain of the function f(x)=sin−1√x−1
View SolutionFind the domain of the function : f(x)=sin−1((log)2x)
View SolutionFind the domain of the function : f(x)=sin−1((log)2x)
View SolutionThe domain of the function f(x)=√4−x2[x]+2 where [x] denotes the greatest integer less than or equal to x,is
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View SolutionThe domain of the functionf(x)=sec−1x√x−[x] , where [x] denotes the greatest integers less than or equal to x is defined for all x belonging to
View Solution
