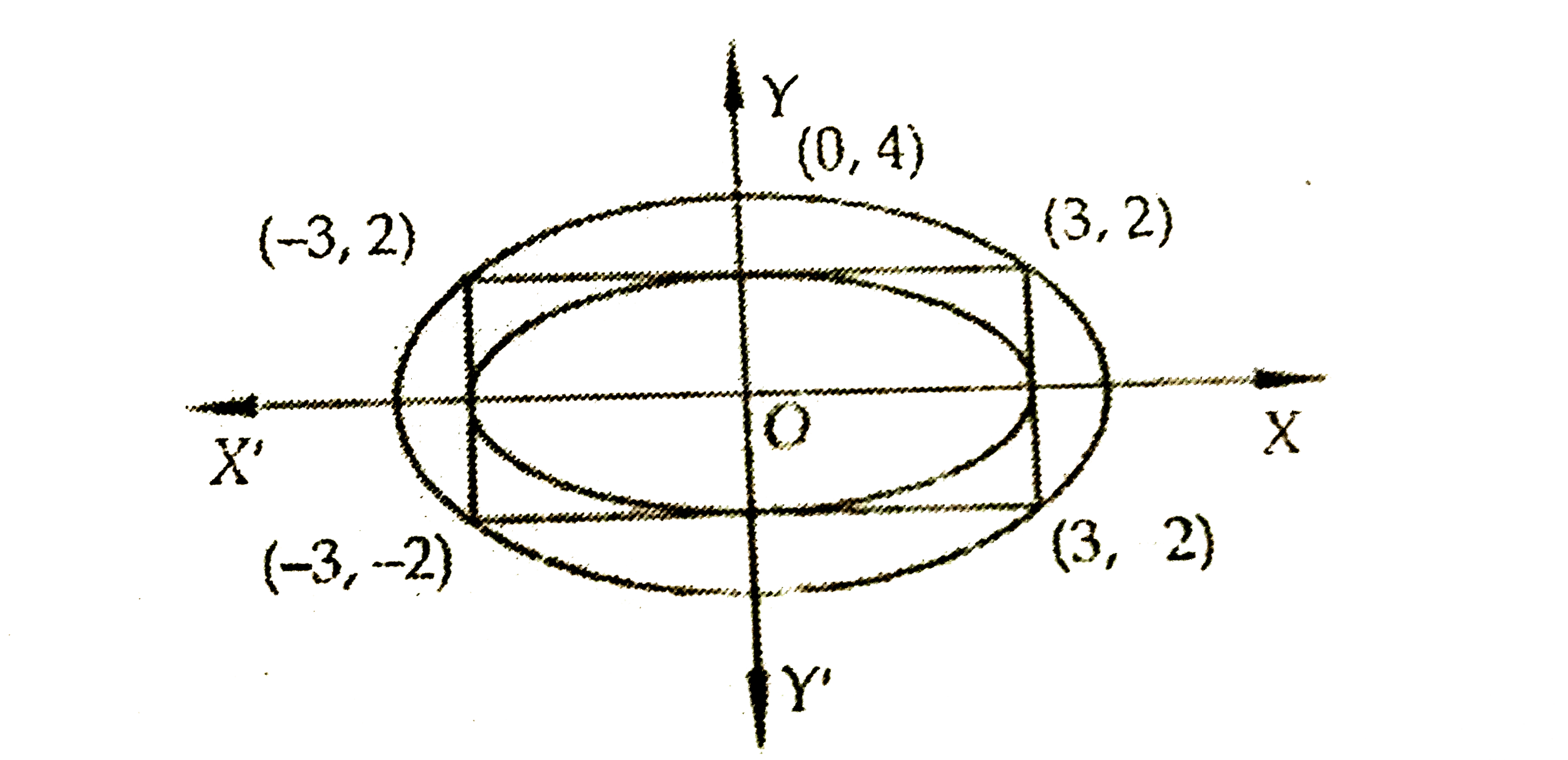
The ellipse $E_{1} : \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ is inscribed in a rectangle $R$ whose sides are parallel to the coordinate axes. Another ellipse $E_{2}$ passing through the point (0, 4) circumscribes the rectangle $R .$ . The eccentricity of the ellipse $E_{2}$ is

$\frac{\sqrt{2}}{2}$

$\frac{\sqrt{3}}{2}$

$\frac{1}{2}$

$\frac{3}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

The ellipse $x^{2} + 4 y^{2} = 4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) $x^{2} + 16 y^{2} = 16$ (2) $x^{2} + 12 y^{2} = 16$ (3) $4 x^{2} + 48 y^{2} = 48$ (4) $4 x^{2} + 64 y^{2} = 48$
A $x^{2} + 12 y^{2} = 16$
B $4 x^{2} + 48 y^{2} = 48$
C $4 x^{2} + 64 y^{2} = 48$
D $x^{2} + 16 y = 16$
The ellipse $x^{2} + 4 y^{2} = 4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) $x^{2} + 16 y^{2} = 16$ (2) $x^{2} + 12 y^{2} = 16$ (3) $4 x^{2} + 48 y^{2} = 48$ (4) $4 x^{2} + 64 y^{2} = 48$
A $x^{2} + 16 y^{2} = 16$
B $x^{2} + 12 y^{2} = 16$
C $4 x^{2} + 48 y^{2} = 16$
D $4 x^{2} + 64 y^{2} = 48$
the equation of the ellipse passing through (2,1) having e=1/2 , is
A $3 x^{2} + 4 y^{2} = 16$
B $3 x^{2} + 5 y^{2} = 17$
C $5 x^{2} + 3 y^{2} = 23$
Dnone of these