The ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The equation of the auxiliary circle of ellipse is
A
x2+y2=6.5
B
x2+y2=5
C
x2+y2=4.5
D
none of these
Video Solution
Text Solution
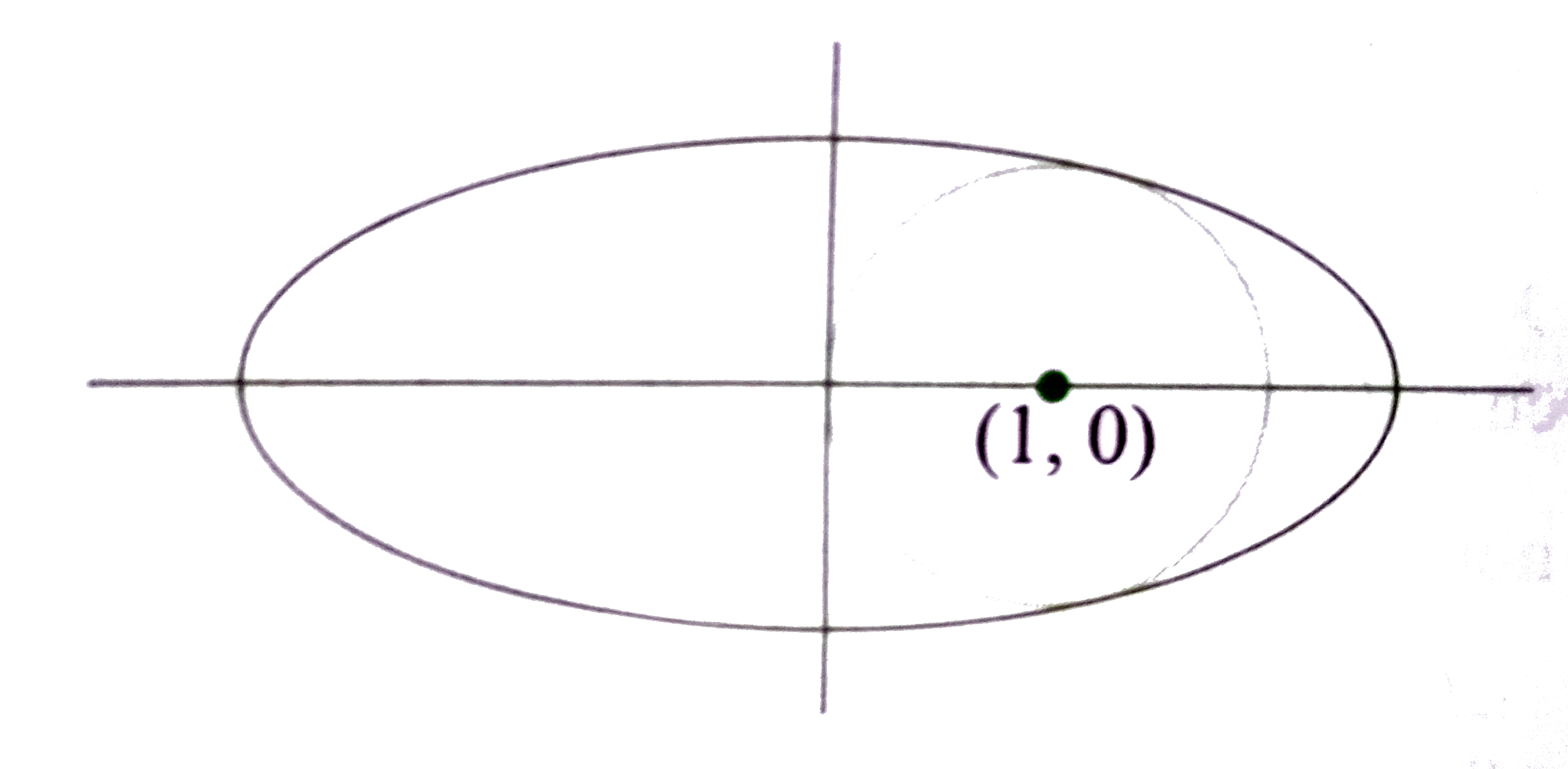
Solving both equations we have
x2a2+1−(x−1)2b2=1
or b2x2+a2[1−(x−1)2]=a2b2
or (b2−a2)x2+2a2x−a2b2=0 (1)
For leat area, the circle.
Therefore, the discriminant of (1) is zero. Thus,
4a2+4a2b2(b2−a2)=0
or a2+b2(b2−a2)=0
or a2+b2(−a2e2)=0
or 1−be2e2=0
orb=1e
Also, a2=b21−e2=1e2(1−e2)
ora=1e√1−e2
Let S be the area of the ellipse. Then,
S=πab=πe2√1−e2=π√e4−e6
The area is minimum if (f)(e)=e2−e6 is maximum, i.e., when f'(e)=4e3−6e5=0
or √23 [ which is the point of maxima for f(e)]
So,S is the least when e=√2/3
Therfore, the ellipse is x2+y2=4.5
Length of loatus rectum of ellipe =2b2a=2×963√2=√2
|
Similar Questions
Knowledge Check
The ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The eccentricity of the ellipse isA(2√2/3)B1√3C1/2Dnone of theseThe ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The length of latus of ellipse isA2 unitsB√2unitsC3 unitsD2.5 unitsThe area of the ellipse x2a2+y2b2=1 is
AπabBπ4(a2+b2)Cπ(a+b)Dπa2b2
If normal at any point P to the ellipse x2a2+y2b2=1(a>b) meets the axes at A and B such that PA:PB=1:2, then the equation of the director circle of the ellipse is
View SolutionEquation of auxilliary circle of ellipse 2x2+6xy+5y2=1 is
View SolutionThe equation of the auxiliary circle of the ellipse x212+y218=1 is
View SolutionThe equation of the auxiliary circle of the ellipse x212+y218=1 is
View SolutionThe area of the ellipse x2a2+y2b2=1 is
View Solution
