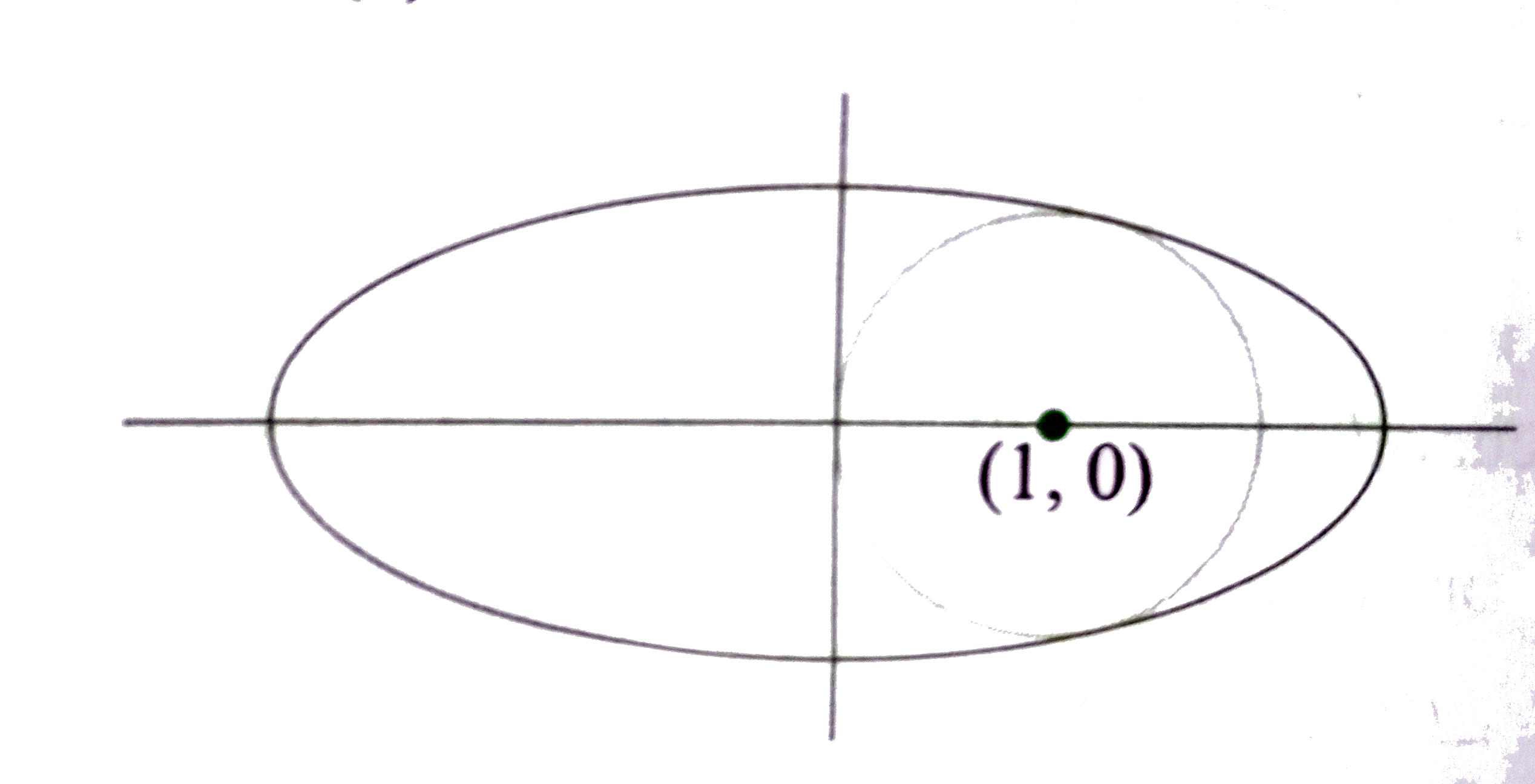
The ellipse is such that its has the least area but contains the circel
The length of latus of ellipse is
A
2 units
B
units
C
3 units
D
units
Video Solution
Text Solution
Solving both equations we have
or
or
For leat area, the circle.
Therefore, the discriminant of (1) is zero. Thus,
or
or
or
Also,
Let S be the area of the ellipse. Then,
The area is minimum if is maximum, i.e., when
or [ which is the point of maxima for f(e)]
So,S is the least when
Therfore, the ellipse is
Length of loatus rectum of ellipe
|
Similar Questions
Knowledge Check
The ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The eccentricity of the ellipse isA(2√2/3)B1√3C1/2Dnone of theseThe ellipse x2a2+y2b2=1 is such that its has the least area but contains the circel (x−1)2+y2=1
The equation of the auxiliary circle of ellipse isAx2+y2=6.5Bx2+y2=5Cx2+y2=4.5Dnone of theseThe area of the ellipse x2a2+y2b2=1 is
AπabBπ4(a2+b2)Cπ(a+b)Dπa2b2
Prove that area common to ellipse x2a2+y2b2=1 and its auxiliary circle x2+y2=a2 is equal to the area of another ellipse of semi-axis aanda−b.
View SolutionThe area of the ellipse x2a2+y2b2=1 is
View SolutionIf the area of the auxiliary circle of the ellipse x2a2+y2b2=1(a>b) is twice the area of the ellipse, then the eccentricity of the ellipse is
View SolutionThe area enclosed by the :
ellipse x2a2+y2b2=1 is :
View SolutionConsider an ellipse x2a2+y2b2=1
What is the length of the latus rectum of the ellipse 25x2+16y2=400?
View Solution
