Doubtnut Promotions Sticky

The equation ex−x−1=0 has

A

one other real root

B

two real roots

C

no other real root

D

infinite number of real roots

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Clearly, curves y=ex and y=x+1 intersect at exactly one-point (0,1).
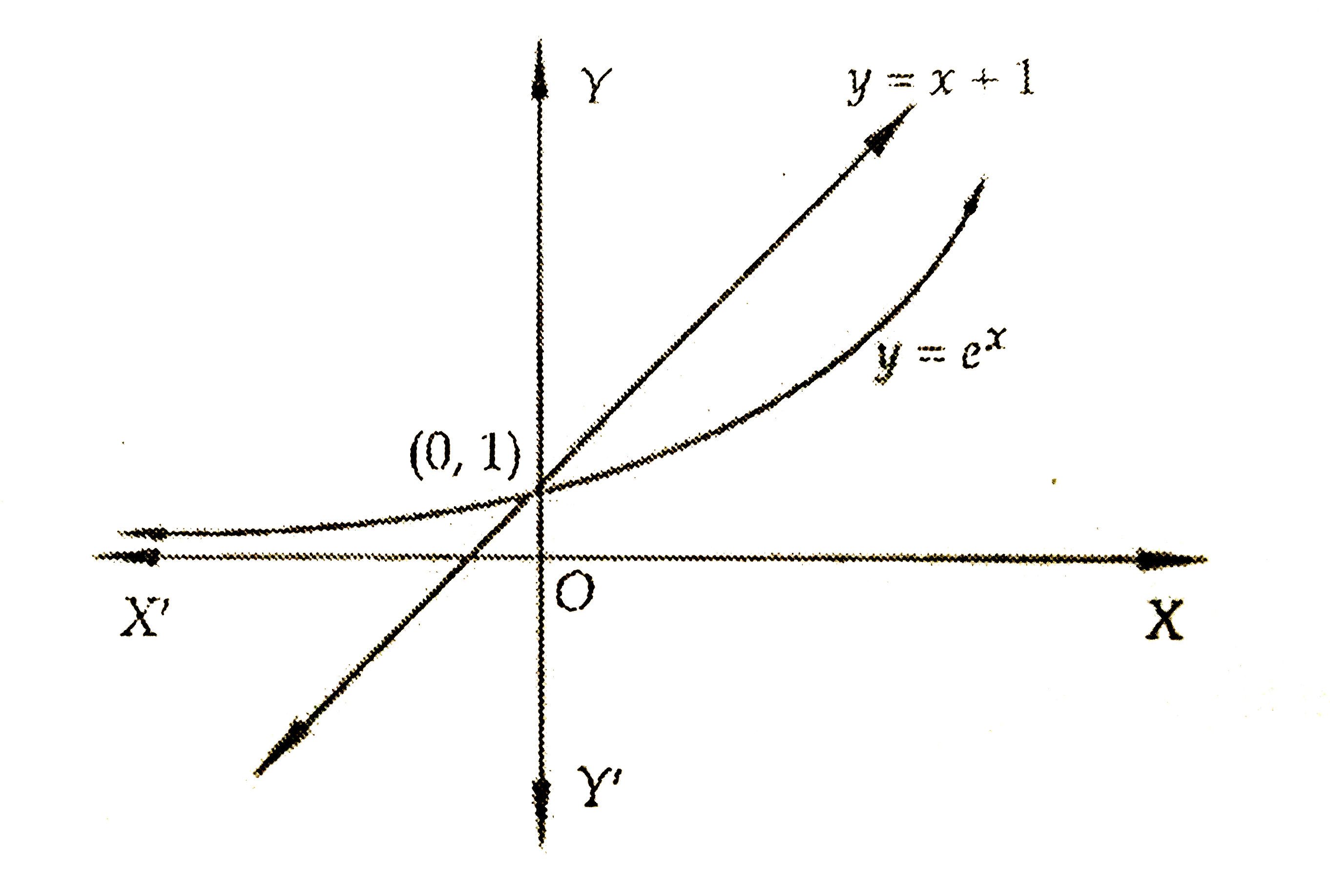
ocr_image
So,ex−x−1=0 has exactly one real root x=0.

|
Updated on:21/07/2023
Class 12MATHSMISCELLANEOUS EQUATIONS AND INEQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Statement-1: The equation ex−1+x−2=0 has only one real root.
    Statement-2 : Between any two root of an equation f(x)=0 there is a root of its derivative f'(x)=0

    AStatement-1 is True, Statement-2 is Ture, Statement-2 is a correct explanation for statement-1
    BStatement-1 is True, Statement-2 is Ture, Statement-2 is not a correct explanation for statement-1
    CStatement-1 is True, Statement-2 is False
    DStatement-1 is False, Statement-2 True.
  • Question 2 - Select One

    The number of real root of the equation ex−1+x−2=0, is

    A1
    B2
    C3
    D4
  • Question 3 - Select One

    Number of real roots of the equation ex−1−x=0 is

    A1
    B2
    C3
    D0