The equation of a line AB is 2x−2y+3=0.
Find the slope of the line AB.
The correct Answer is:1
To find the slope of the line given by the equation 2x−2y+3=0, we will convert the equation into the slope-intercept form, which is y=mx+c, where m represents the slope.
1. Start with the given equation:
2x−2y+3=0
2. Rearrange the equation to isolate y:
- First, move 2x and 3 to the right side:
−2y=−2x−3
3. Divide the entire equation by −2 to solve for y:
y=−2x−2+−3−2
Simplifying this gives:
y=x+32
4. Identify the slope m:
- From the equation y=mx+c, we see that the slope m is the coefficient of x:
m=1
Final Answer:
The slope of the line AB is 1.
---
2x−2y+3=0
- First, move 2x and 3 to the right side:
−2y=−2x−3
y=−2x−2+−3−2
Simplifying this gives:
y=x+32
- From the equation y=mx+c, we see that the slope m is the coefficient of x:
m=1
The slope of the line AB is 1.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - EQUATION OF A LINEEXERCISE - EXERCISE 14(E)68videos
EQUATION OF A LINE
- BOOK - ICSECHAPTER - EQUATION OF A LINEEXERCISE - EXERCISE 14(C)32videos
EQUATION OF A LINE
- BOOK - ICSECHAPTER - CYLINDER, CONE AND SPHERE EXERCISE - EXERCISE 20 (G)23videos
CYLINDER, CONE AND SPHERE
- BOOK - ICSECHAPTER - FACTORISATIONEXERCISE - M.C.Q(Competency Based Questions )15videos
FACTORISATION
Similar Questions
The equation of a line is 3x+4y−7=0. Find:
the slope of the line.View SolutionThe equation of a line AB is 2x−2y+3=0.
Calculate the angle that the line AB makes with the positive direction of the x-axis.View SolutionThe equation of a line is 3x+4y−7=0. Find:
the equation of a line perpendicular to the given line and passing through the intersection of the lines x−y+2=0 and 3x+y−10=0.View SolutionThe equation of the line AB is y=x. If A and B lie on the same side of the line mirror 2x−y=1, then the equation of the image of AB is
View SolutionEquation of straight line is 2x+3y=5. Slope of the straight line is :
View SolutionThe drawn alongiside (not drawn to scale) shows two stragit lines AB and CD. If the equation of line AB is: x−√3y+5=0 and the equation of line CD is : x−y=2, write down the inclinations of lines AB and CD, also find the angle θ i.e., angle CPB.
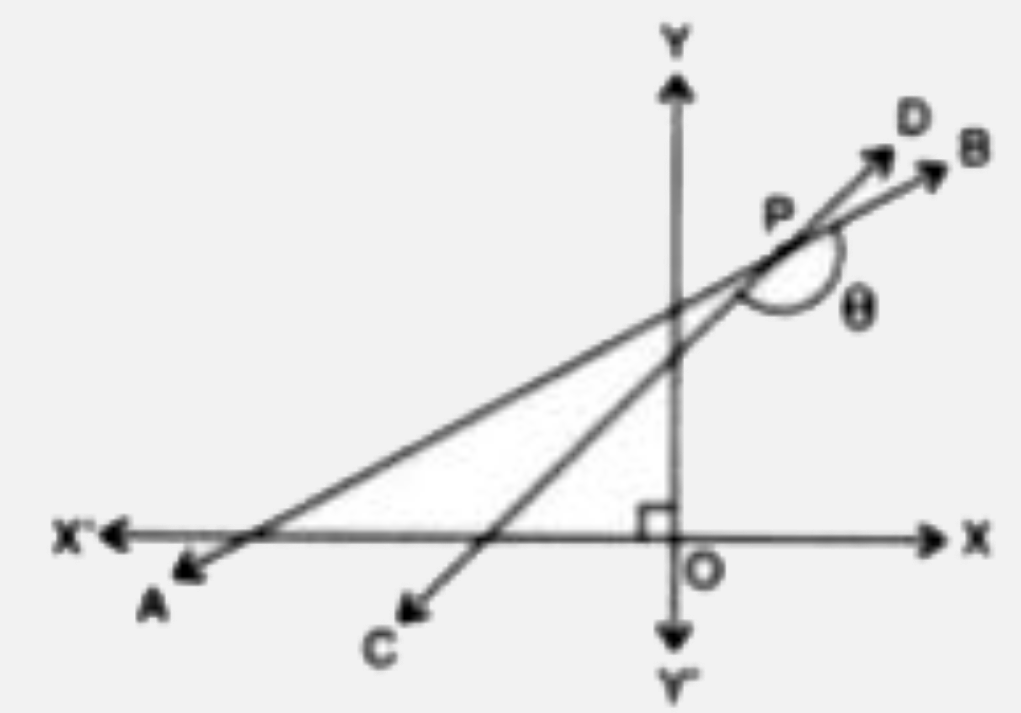 View Solution
View SolutionThe equation of a line is 3x−4y+12=0. It meets the x-axis at point A and the y-axis at point B. Find :
the length of intercept AB, cut by the line within the co-ordinate axes.View SolutionEquation of a line is 3x−4y+10=0. Find its (i) slope, (ii) x and yintercepts.
View SolutionThe given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y=x+1 and equation of line CD is : y=√3x−1. Write down the inclination of lines AB and CD, also, find the angle θ between AB and CD.
 View Solution
View SolutionFind the equation of a line whose :
y-intercept = 2 and slope = 3.View Solution

