The equation of the straight line which passes through the point (−4,3) such that the portion of the line between the axes is divided internally be the point in the ratio 5:3 is (a) 9x−20y+96=0 (b) 9x+20y=24 (c) 20x−9y+53=0 (d) none of these
The correct Answer is:N/a
Since, the line intersects X and Y -axes respectively at A(x,0)and B (0,y).
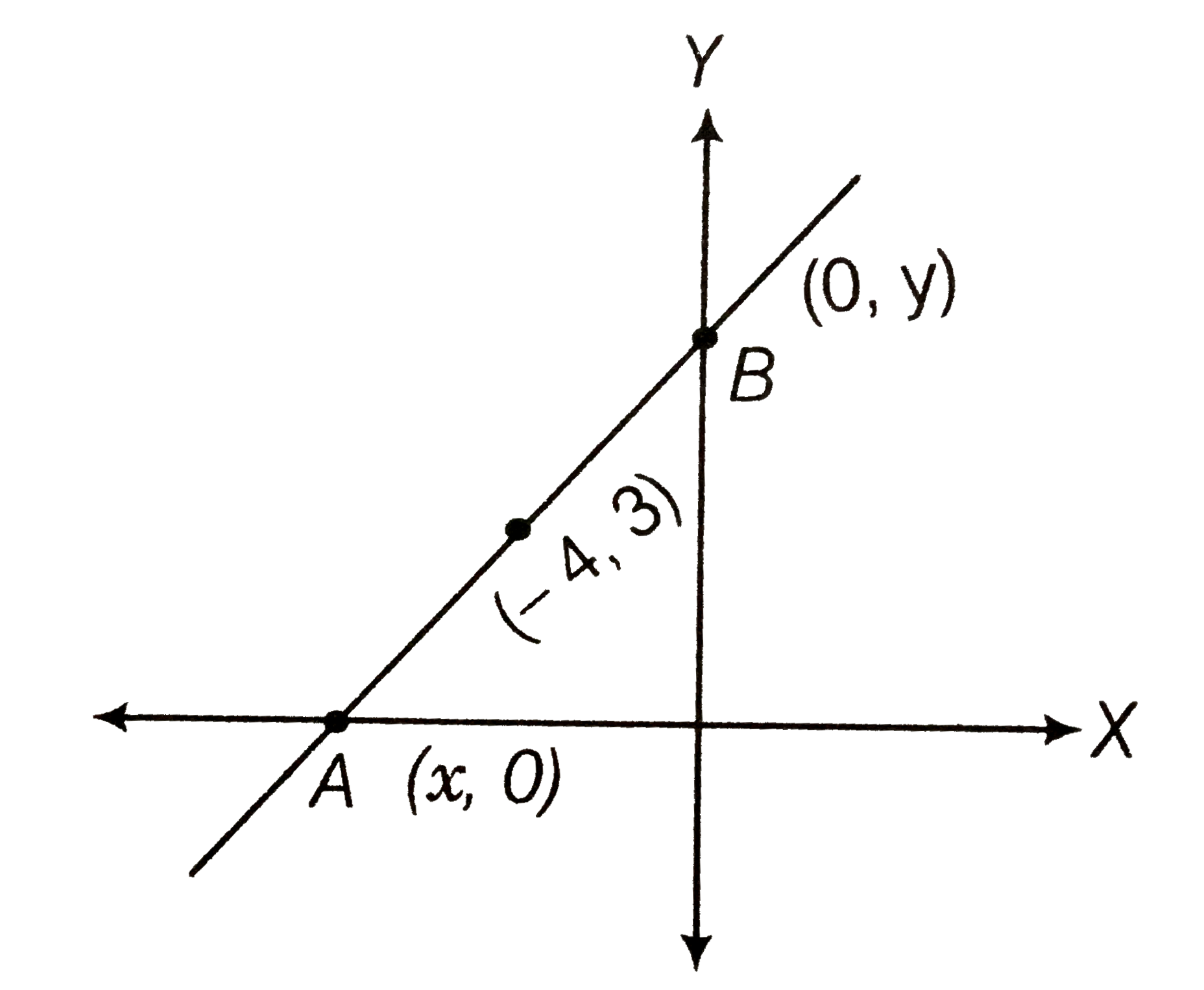
4=5×0+3x5+3
⇒−4=3x8⇒x=−323
and 3=5.y+3.05+3
⇒3=5y8⇒y=245
Since, the intercept on the Xand Y-axes respectively are a =−323 and b=245
∴ Equation of required line is x−32/3+y24/5=1
⇒−3x32+5y24=1
⇒−9x+20y=96
⇒9x−20y+96=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Objective type questions
20 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Fillers
6 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - MATCHING THE COLUMN
3 Videos
- STATISTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE
9 Videos
Similar Questions
The equation of the straight line which passes through the point (−4,3) such that the portion of the line between the axes is divided internally be the point in the ratio 5:3 is (A)9x−20y+96=0 (B) 9x+20y=24 (C) 20x+9y+53=0 (D) None of these
View SolutionThe equation of the straight line which passes through the point (−4,3) such that the portion of the line between the axes is divided internally be the point in the ratio 5:3 is 9x−20y+96=0 9x+20y=24 20x−9y+53=0 none of these
View SolutionThe equation of straight line which passes through the point (-4,3) such that the portion of the line between the axes is divided by the point in ratio 5:3 is -
View SolutionThe equation of straight line which passes through the point (-4,3) such that the portion of the line between the axes is divided by the point in ratio 5:3 is -
View SolutionThe equation of straight line which passes through the point (-4,3) such that the portion of the line between the axes is divided by the point in ratio 5:3 is -
View SolutionFind the equation of the straight line which passes through the point (4, 5) and is parallel to 3x+ 4y = 5
View SolutionFind the equation of the straight line which passes through the point (2,−3) and the point intersection of the lines x+y+4=0and3x−y−8=0.
View SolutionFind the equation of the straight line which passes through
the point (2, -9) and the intersection of the lines 2x+5y−8=0and3x−4y=35
View SolutionFind the equation of the straight line which passes through the point (2,−2) and the point of intersection of the lines 5x−y=9andx+6y=8.
View SolutionFind the equation of the straight line that passes through the point (3,4) and is perpendicular to the line 3x+2y+5=0
View Solution
