Question

The equations of bisectors of the angles between the lines ${\displaystyle \left|x\right|=\left|y\right|}$ are

Options

A. `y = pmx,x=0`
B. `x=(1)/(2), y=(1)/(2)`
C. `y=0,x=0`
D. none of these

Answer

C

Explanation

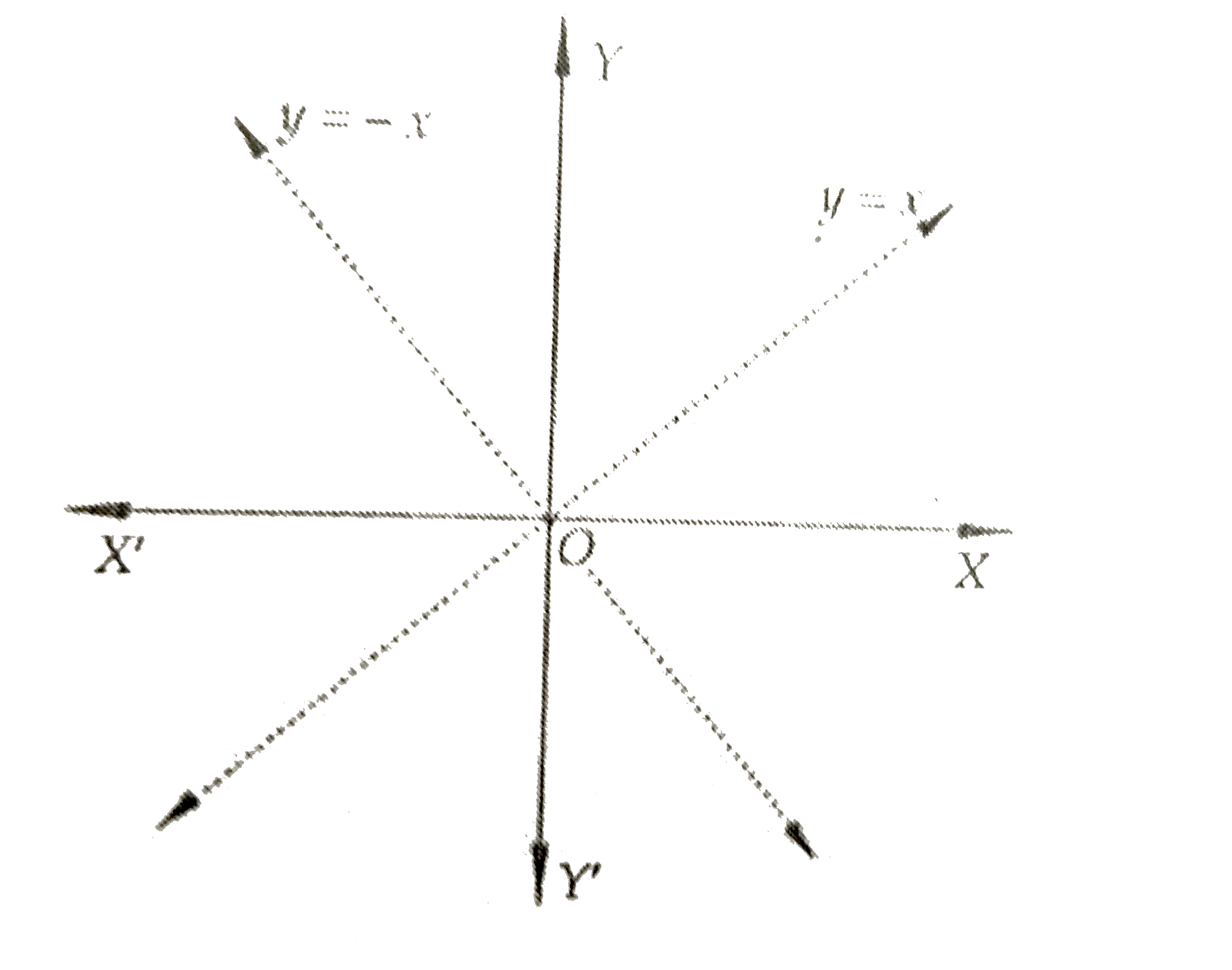
Given lines are `|x|=|y|` or `y=pmx`. Clearly , these are the bisectors of the first and second quadrant angles. So, the bisectors of the angles between these lines are the coordinate axes i.e. x=0, y=0.