The equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
The correct Answer is:14x+23y-40=0
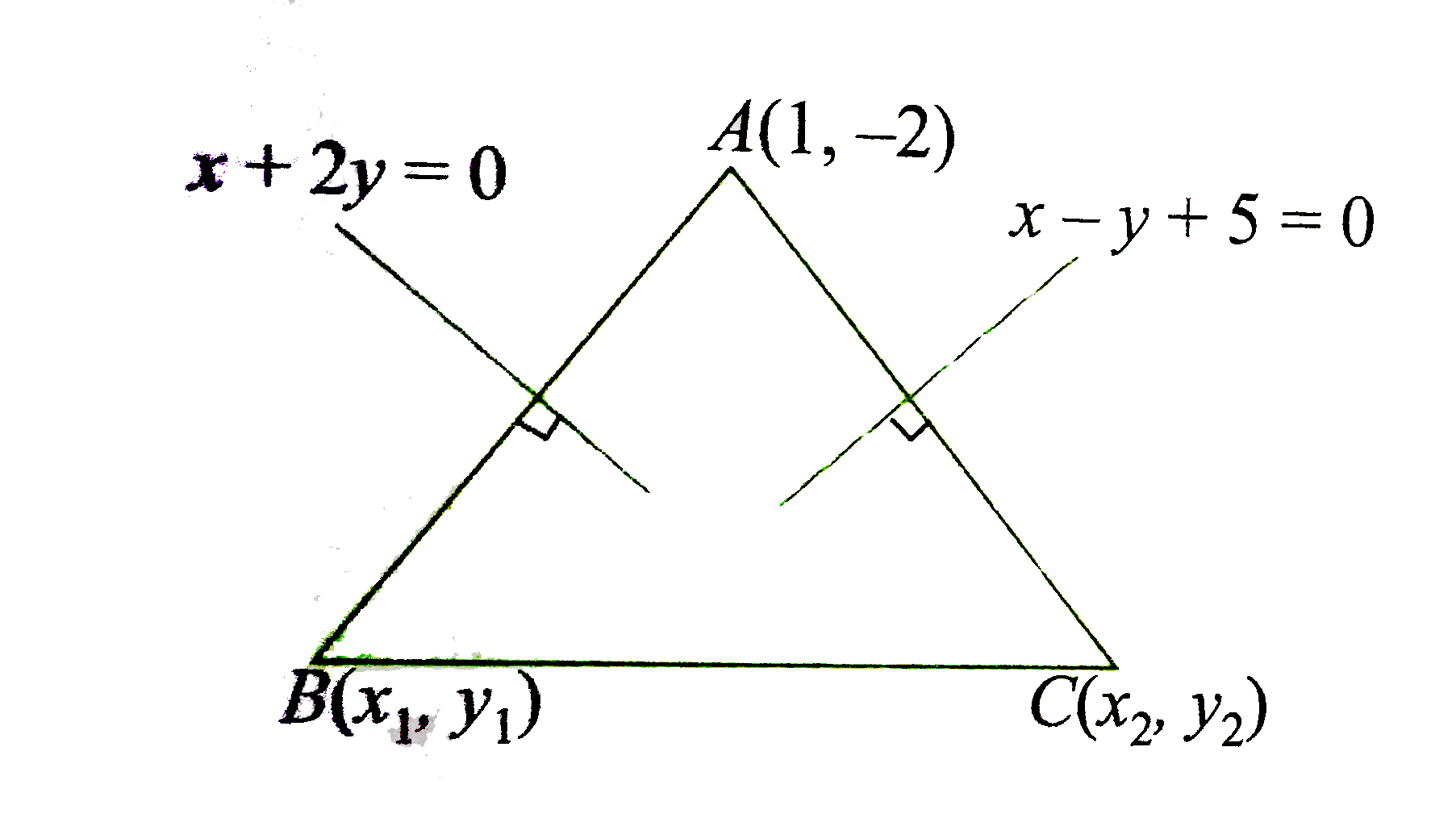
Since the given lines are perpendicular bisectors of the sides as shown in the figure, point B and C are the images of the point A in these lines. Therefore,
x1−11=y1−22=−2(1−4)1+4
and x2−11=y2+2−1=−2(1+2+5)1+1
∴B(x1,y1)≡(11/5,2/5) and C(x2,y2)≡(−7,6)
Hence, the line passing through the points B and C is 14x+23y-40=0.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Single)82videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.48videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
The equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe equations of the perpendicular bisector of the sides AB and perpendicular bisector of the sides AB and AC of a △ABC are x-y + 5 = 0 and x + 2y = 0 respectively, if the point Ais (1,-2), then the equation ofthe line BC is
View Solution
Knowledge Check
- Question 1 - Select One
The equations of perpendicular bisectors of the sides AB and AC of a triangle ABC are x−y+5=0 and x+2y=0 respectively
If the point A is (1,-2) the equation of the line BC isA23x+4y−40=0B23x+14y+40=0C14x+23y−40=0D14x+23y+40=0 - Question 2 - Select One
The equations of perpendicular bisectors of the sides AB and AC of a ΔABC are x−y+5=0 and x+2y=0, respectively. If the point A is (1, - 2) the equation of the line BC is
A23x+14−40=0B23+14y+40=0C14x+23y−40=0D14x+23y+40=0 - Question 3 - Select One
The equations of perpendicular bisectors of the sides AB and AC of a ΔABC are x−y+5=0 and x+2y=0, respectively. If the point A is (1, - 2) the equation of the line BC is
A23x+14y−40B23x+14y+40=0C14x+23y−40=0D14x+23y+40=0
The equations of the perpendicular bisectors of the sides AB&AC of a triangle ABC are x−y+5=0&x+2y=0. find the equation of the bc
View Solutionthe equation of perpendicular bisectors of side AB,BC of triangle ABC are x−y=5,x+2y=0 respectively and A(1,−2) then coordinate of C
View SolutionThe equations of perpendicular bisectors of two sides AB and AC of a triangle ABC are x+y+1=0 and x−y+1=0 respectively. If circumradius of Δ ABC is 2 units, then the locus of vertex A is
View SolutionThe equation of the perpendicular bisector of the side AB of a triangle ABC is x−y+5=0. If the point A is (1,2), find the co-ordinates of the point B.
View SolutionThe equation of perpendiculars of the sides AB and AC of triangle ABC are x−y−4=0 and 2x−y−5=0 respectively. If the vertex A is (-2,3) and point of intersection of perpendicular bisectors is (32,52) find the equation of medians to the sides AB& AC respectively
View Solution

