The feasible solution for a LPP is hown as below,
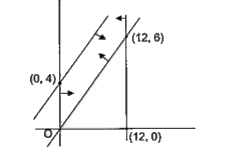
Let Z =3x -4y be the objective function . Then, Minimum of Z occurs at
(0,0)
(0,8)
(5,0)
(4,10)
The correct Answer is:B
From the above table the minimum value of z is -32 which occurs at point (0, 8).
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
The feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
 A(0,0)B(0,8)C(5,0)D(4,10)
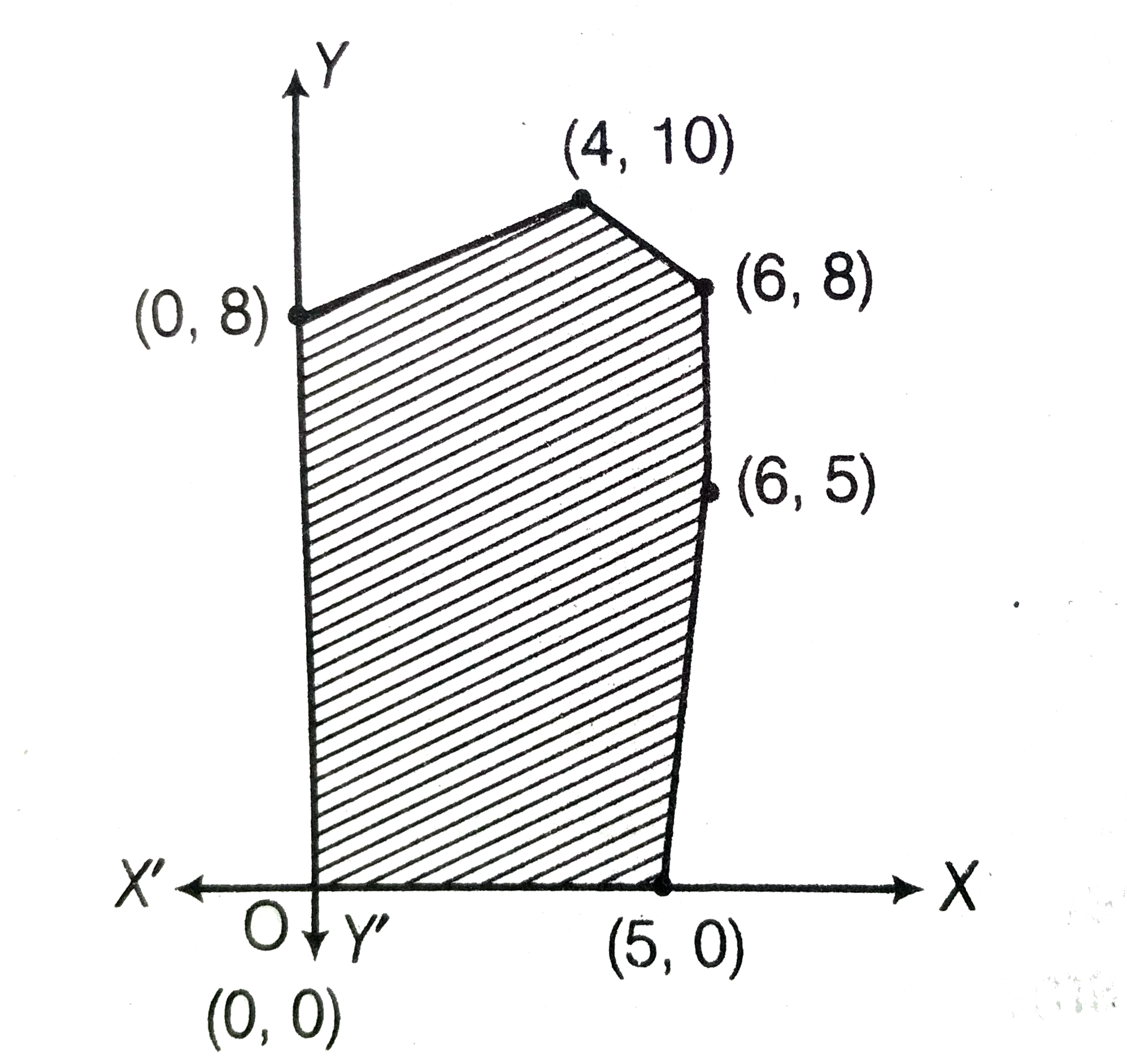
A(0,0)B(0,8)C(5,0)D(4,10)The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
 A0B8C12D−18
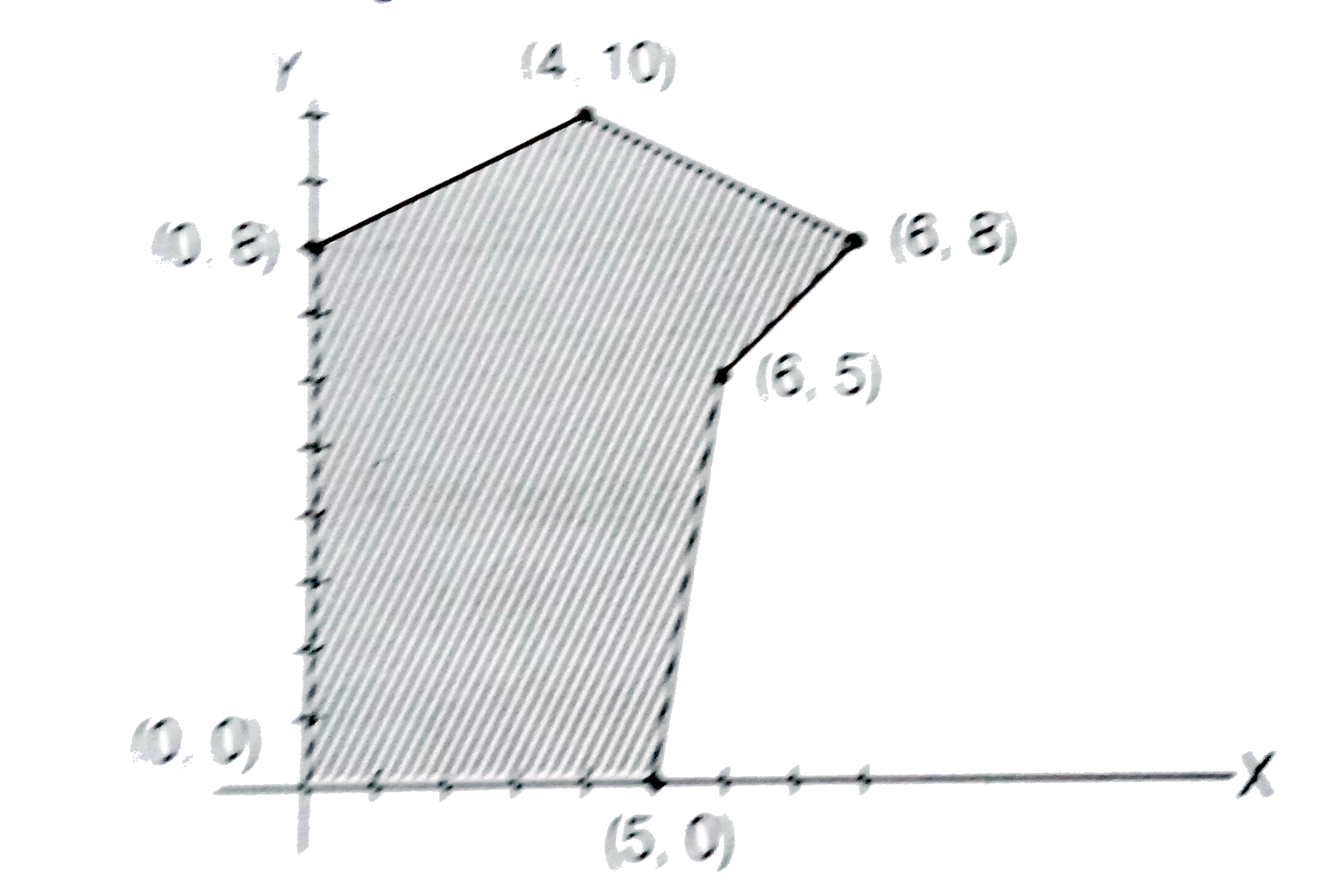
A0B8C12D−18Corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F=4x+6y be the objective function. Determine the minimum value of F occurs at
Aonly (0,2)Bonly (3,0)Cthe mid point of the line segment joining the points (0,2) and (3,0)Dany point of the line segment joining the points (0,2) and (3,0)
The feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
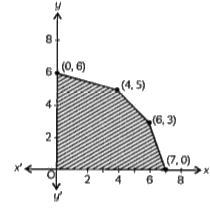
View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
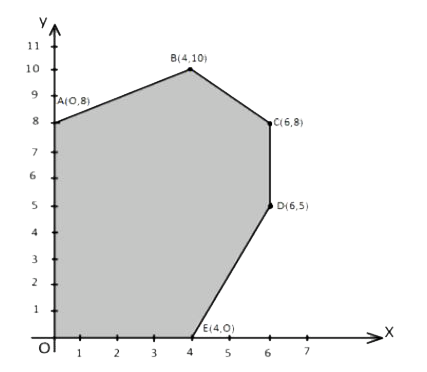
Let Z=3x−4y be the objective function. Find the maximum and minimum value of Z and also the corresponding points at which the maximum and minimum value occurs.
View SolutionIf the feasibile region for a LPP is undoubed, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionLet R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false?
View SolutionIn the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
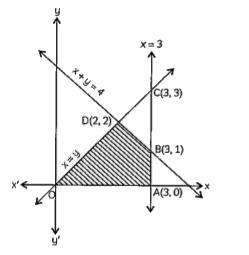
View Solution