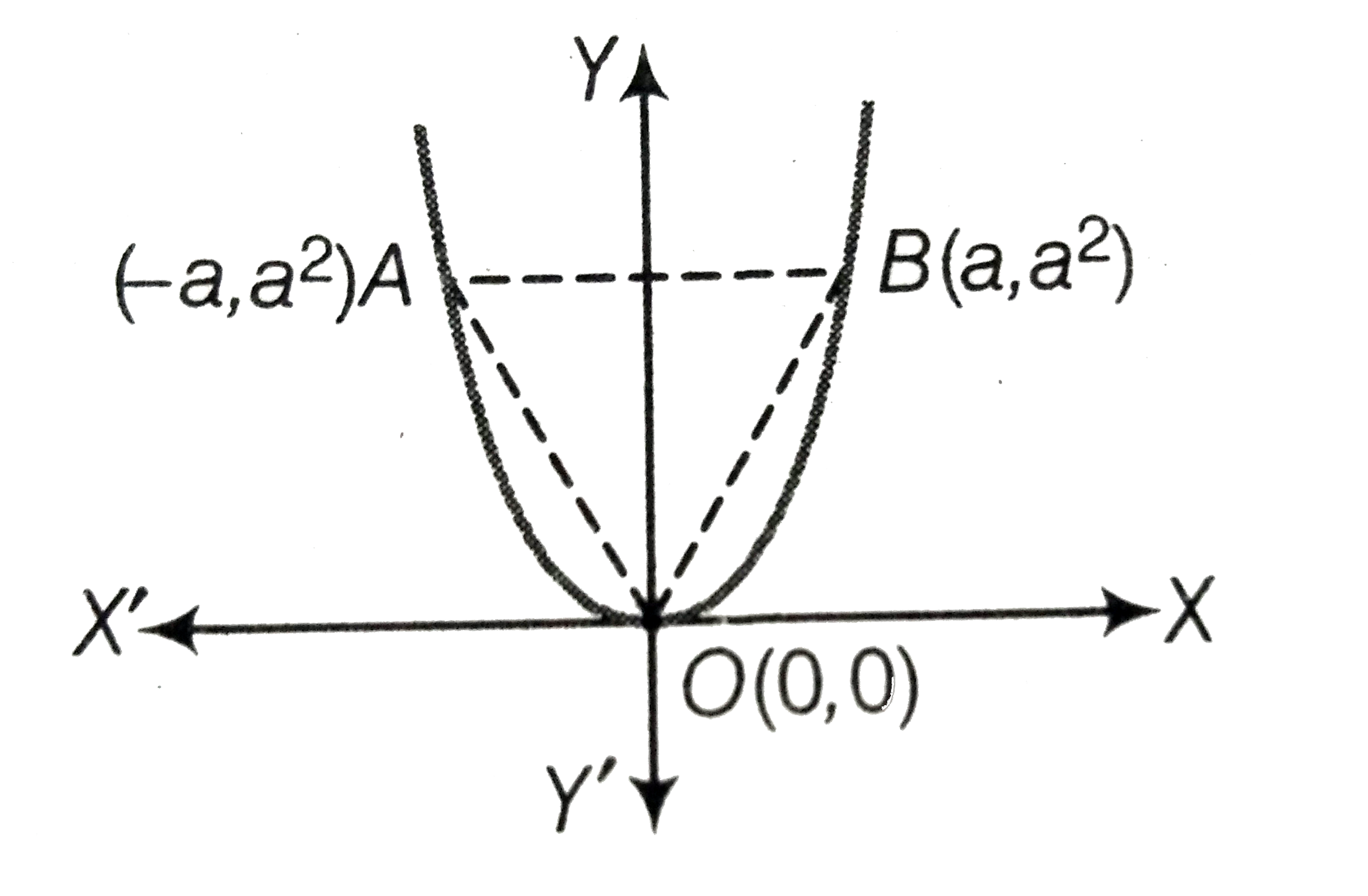
The figure shows a $Δ A O B$ and the parabola $y = x^{2}$ . The ratio of the area of the $Δ A O B$ to the area of the region AOB of the parabola $y = x^{2}$ is equal to

$\frac{3}{5}$

$\frac{3}{4}$

$\frac{7}{8}$

$\frac{5}{6}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for The figure shows a DeltaAOB and the parabola y = x^(2). The ratio of the area of the DeltaAOB to the area of the region AOB of the parabola y = x^(2) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
The area of the region bounded by y – x = 2 and $x^{2} = y$ is equal to
A $\frac{16}{3}$
B $\frac{2}{3}$
C $\frac{9}{2}$
D $\frac{4}{3}$
Question 2 - Select One
The area of the region bounded by the parabola $y = x^{2}$ and the line y = 4x is
A $\frac{32}{3} s q . u n i t s$
B $\frac{16}{3} s q . u n i t s$
C $\frac{8}{3} s q . u n i t s$
D $\frac{4}{3} s q . u n i t s$

DISHA PUBLICATION-APPLICATION OF INTEGRALS-EXERCISE-1: CONCEPT BUILDER (TOPICWISE)

Home
Ask Doubt
Profile

The figure shows a Δ A O B and the parabola y = x 2 . The ratio of the area of the Δ A O B to the area of the region AOB of the parabola y = x 2 is equal to

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the region bounded by y – x = 2 and x2=y is equal to

The area of the region bounded by the parabola y=x2 and the line y = 4x is

DISHA PUBLICATION-APPLICATION OF INTEGRALS-EXERCISE-1: CONCEPT BUILDER (TOPICWISE)

The figure shows a $Δ A O B$ and the parabola $y = x^{2}$ . The ratio of the area of the $Δ A O B$ to the area of the region AOB of the parabola $y = x^{2}$ is equal to

The area of the region bounded by y – x = 2 and $x^{2} = y$ is equal to

The area of the region bounded by the parabola $y = x^{2}$ and the line y = 4x is