The foci of an ellipse are and The normal at P is Then point P is
The correct Answer is:(17,1)
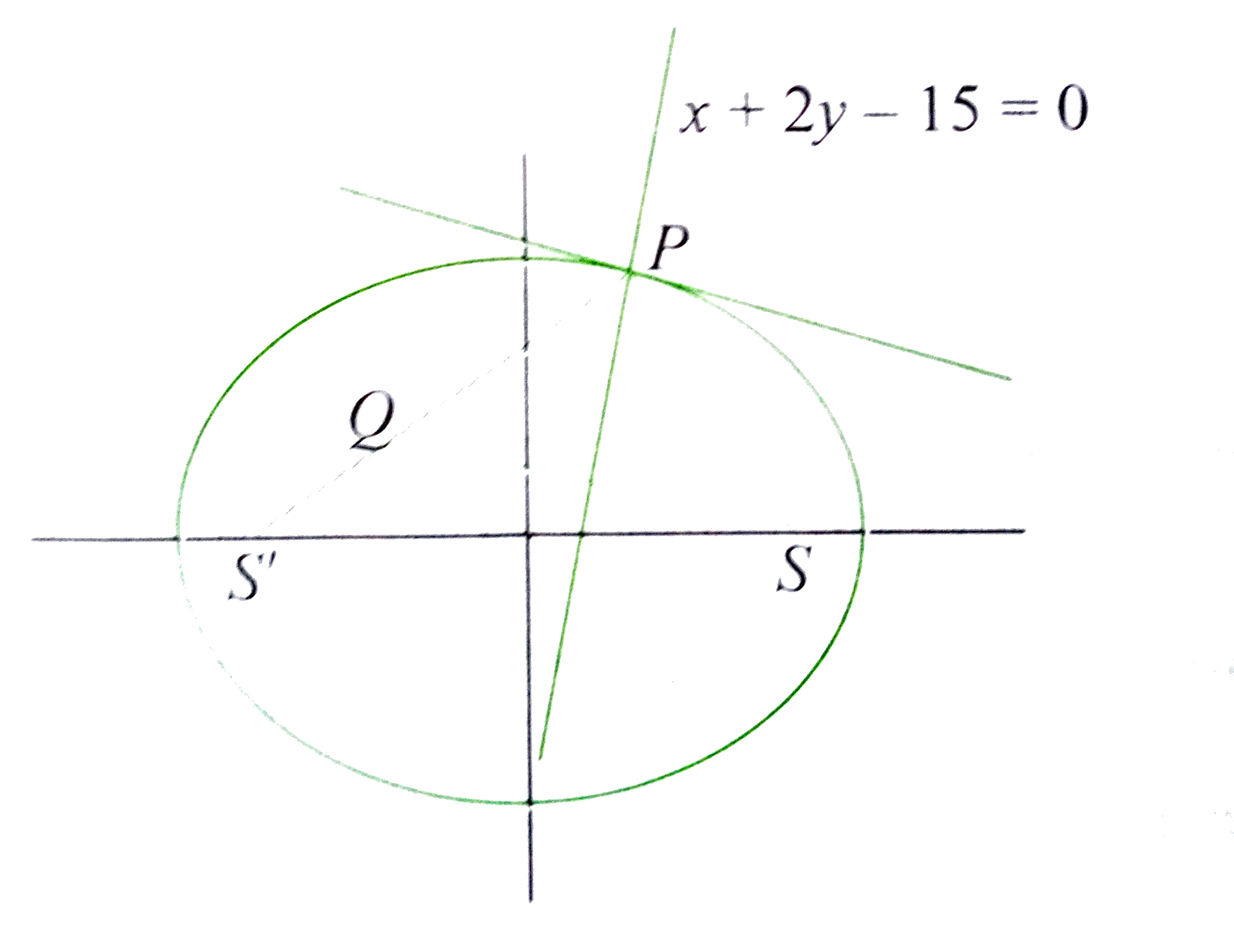
We know that normal at P bisects
Thus, the image of S w.r.t.x+2y-15=0 lies on S'P.
Now, image of S(3,1) w.r.t.x+2y-15 ius Q(7,9).
Equation of S'Q is x+y-16=-0
Clearly, from the figure, P is point of intersection of S'Q and normal, which is (17,-1)
Similar Questions
The coordinates of the foci of an ellipse are S(3,4) and S(2,−3). If P is a point on the ellipse such that PS+PS'=K, then (A) K>5 (B) K>5√2 (C) K<5 (D) 5<K<5√2
View SolutionFoci of an ellipse are at S(1,7),S'(1,-3) .The point P is on the ellipse such that SP=7,S'P=5 .then the equation of the ellipse is
View Solution
Knowledge Check
If foci of an ellipse are (−2,3),(5,9) & 2x+3y+15=0 is tangent to the ellipse. Then find the point of contact the tangent cannot be
A(72,−1)B(−92,−2)C(−1,92)D(−1,72)The points (1,−1) and (2,−1)are the foci of an ellipse and the line x+y=5 is a tangent to this ellipse. The point of contact of the tangent is
A(349,119)B(329,139)C(−349,799)D(−329,779)if S and S are two foci of an ellipse x2a2+y2b2=1 ( altb) and P(x1,y1) a point on it then SP+ S'P is equal to
A2aB2bCa+ex1Db+ey1
S1,S2, are foci of an ellipse of major axis of length 10units and P is any point on the ellipse such that perimeter of triangle PS1S2, is 15. Then eccentricity of the ellipse is:
View SolutionWhich of the following is/are true about the ellipse x2+4y2−2x−16y+13=0? the latus rectum of the ellipse is 1. The distance between the foci of the ellipse is 4√3. The sum of the focal distances of a point P(x,y) on the ellipse is 4. Line y=3 meets the tangents drawn at the vertices of the ellipse at points P and Q . Then PQ subtends a right angle at any of its foci.
View Solution(i) Find the point on the curve 9y2=x3 where normal to the curve has non zero x -intercept and both the x intercept and y- intercept are equal.
(ii) If the tangent at (1,1) on y2=x(2−x)2 meets the curve again at P, then find coordinates of P
(iii) The normal to the curve 5x5−10x3+x+2y+6=0 at the point P(0,-3) is tangent to the curve at some other point (s). Find those point(s)?
View SolutionIf F1andF2 be the feet of the perpendiculars from the foci S1andS2 of an ellipse x25+y23=1 on the tangent at any point P on the ellipse then (S1F1)(S2F2) is equal
View SolutionIf the foci of the ellipse x29+y2=1 student a right angle at a point P. Then, the locus of P is
View Solution