The foci of an ellipse are S(3,1) and S'(11,5)The normal at P is x+2y−15=0 Then point P isSolution in Bengali
a) 17,1
b) -17,-1
c) -17,1
d) 17,-1
The correct Answer is:(17,1)
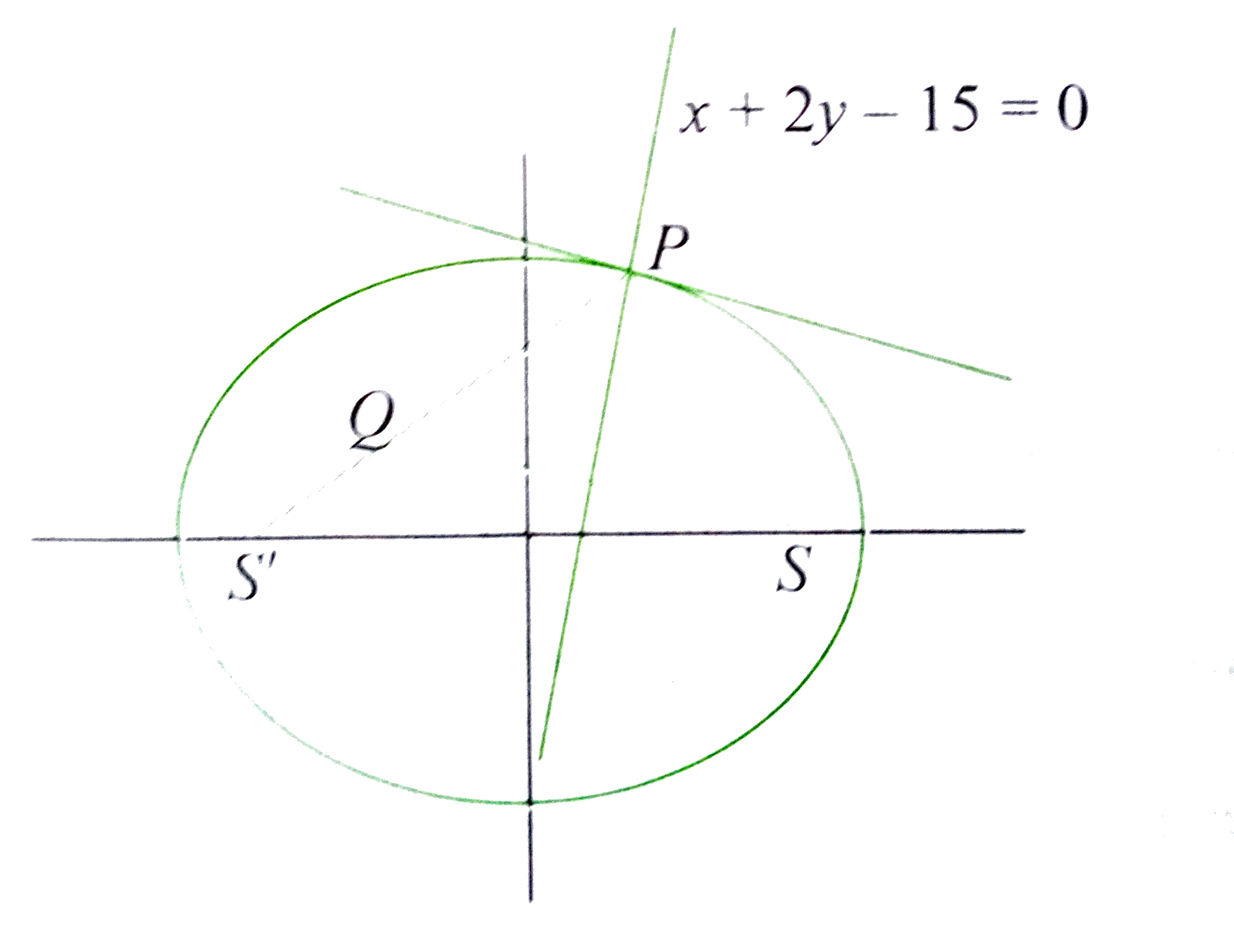
We know that normal at P bisects ∠SPS'
Thus, the image of S w.r.t.x+2y-15=0 lies on S'P.
Now, image of S(3,1) w.r.t.x+2y-15 ius Q(7,9).
Equation of S'Q is x+y-16=-0
Clearly, from the figure, P is point of intersection of S'Q and normal, which is (17,-1)
Similar Questions
P is a point on the ellipse x236+y29=1; S,S1 are the Foci of the ellipse then SP+S1P =
View SolutionP is a point on the ellipse x2a2+y2b2=1 S and S1 are foci A & A1 are the vertices of the ellipse then the ratio ∣∣∣SP−S1PSP+S1P∣∣∣ is
View SolutionLet S and S1 be the foci of an ellipse . At any point P on the ellipse if SPS1<90∘ then its eccentricity :
View SolutionA,A1 are the vertices , S, S1 are the foci of an ellipse . The tangent at any point 'P' on the ellipse is the external angular bisector of
View SolutionThe foci of an ellipse are S(3,1) and S'(11,5)The normal at P is x+2y−15=0 Then point P is
View SolutionThe P is any point on the ellipse 4x2+16y2=64 whose foci are S and S′, then SP+S′P=
View SolutionIf P is any point on the ellipse 9x2+36y2=324 whose foci are S and S'. Then, SP + S' P equals
View SolutionLet S and S\' be the foci of the ellipse x^2/9 + y^2/4 = 1 and P and Q be points on the ellipse such that PS.PS\' is maximum and QS.QS \' is maximum. Statement 1 : PQ=4 . Statement 2 : If P is a point on an ellipse and S\' and S are its foci, then PS + PS\' is constant.
View Solution
