The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.
To find the missing frequency f given that the mean pocket allowance is Rs 18, we can follow these steps:
Step 1: Understand the Mean Formula
The mean of a frequency distribution is calculated using the formula:
Mean=∑(fi⋅xi)∑fi
where fi is the frequency and xi is the mid-value of the class intervals.
Step 2: Identify the Data
Let's assume the distribution of daily pocket allowance is as follows (with f as the missing frequency):
| Pocket Allowance (Rs) | Frequency (fi) |
|------------------------|-----------------------|
| 11 - 13 | 7 |
| 13 - 15 | 6 |
| 15 - 17 | 9 |
| 17 - 19 | 13 |
| 19 - 21 | f |
| 21 - 23 | 5 |
| 23 - 25 | 4 |
Step 3: Calculate Mid-values (xi)
Calculate the mid-values for each class interval:
- For 11 - 13: x1=11+132=12
- For 13 - 15: x2=13+152=14
- For 15 - 17: x3=15+172=16
- For 17 - 19: x4=17+192=18
- For 19 - 21: x5=19+212=20
- For 21 - 23: x6=21+232=22
- For 23 - 25: x7=23+252=24
Step 4: Calculate fi⋅xi
Now calculate fi⋅xi for each class:
- 12⋅7=84
- 14⋅6=84
- 16⋅9=144
- 18⋅13=234
- 20⋅f=20f
- 22⋅5=110
- 24⋅4=96
Step 5: Sum Up fi⋅xi and fi
Now sum these values:
∑(fi⋅xi)=84+84+144+234+20f+110+96=752+20f
Sum of frequencies:
∑fi=7+6+9+13+f+5+4=44+f
Step 6: Set Up the Mean Equation
We know the mean is 18, so we set up the equation:
18=752+20f44+f
Step 7: Cross-Multiply to Solve for f
Cross-multiplying gives:
18(44+f)=752+20f
Expanding this:
792+18f=752+20f
Step 8: Rearranging the Equation
Rearranging the equation:
792−752=20f−18f
40=2f
Step 9: Solve for f
Dividing both sides by 2:
f=20
Final Answer
The missing frequency f is 20.
---
The mean of a frequency distribution is calculated using the formula:
Mean=∑(fi⋅xi)∑fi
where fi is the frequency and xi is the mid-value of the class intervals.
Let's assume the distribution of daily pocket allowance is as follows (with f as the missing frequency):
|------------------------|-----------------------|
| 11 - 13 | 7 |
| 13 - 15 | 6 |
| 15 - 17 | 9 |
| 17 - 19 | 13 |
| 19 - 21 | f |
| 21 - 23 | 5 |
| 23 - 25 | 4 |
Calculate the mid-values for each class interval:
- For 11 - 13: x1=11+132=12
- For 13 - 15: x2=13+152=14
- For 15 - 17: x3=15+172=16
- For 17 - 19: x4=17+192=18
- For 19 - 21: x5=19+212=20
- For 21 - 23: x6=21+232=22
- For 23 - 25: x7=23+252=24
Now calculate fi⋅xi for each class:
- 12⋅7=84
- 14⋅6=84
- 16⋅9=144
- 18⋅13=234
- 20⋅f=20f
- 22⋅5=110
- 24⋅4=96
Now sum these values:
∑(fi⋅xi)=84+84+144+234+20f+110+96=752+20f
∑fi=7+6+9+13+f+5+4=44+f
We know the mean is 18, so we set up the equation:
18=752+20f44+f
Cross-multiplying gives:
18(44+f)=752+20f
Expanding this:
792+18f=752+20f
Rearranging the equation:
792−752=20f−18f
40=2f
Dividing both sides by 2:
f=20
The missing frequency f is 20.
Similar Questions
CH. 14 STATISTICS Q1 Class 0-8 8-16 16-24 24-32 32-40 Frequency 10 12 26 9 15 e mean of above data by: () Direct method () Assumed mean method (ii) Step deviati iop metod. Q2 The following distribution shows the daily pocket allowance of children of a locali ty. The mean pocket allowance is Rs 20. Find the missing frequency Daily Pocket 0-20 20-40 40-60 0-80 80-100 No. Of Children 7 10 9 13 Q3. The following table shows age distribution of persons in a particular region. Find the: (0) mean age (i)modal age (ili) median age Age→ Below!0 Below20 Below30 Below 40, Below 50 Belo No, persons → 250 190 100 40 15 4 Arithmetic mean of the following frequency distribution is 50. Find the missing frequencies C.I. → 0-20 20-40 40-60 60-80 80-100 Tota
View SolutionMean pocket allowance is Rs18. Find the missing frequency k.
View SolutionThe following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.
View SolutionThe following table represent pocket allowance of children of a colony. The mean pocket allowance is Rs 18. Find missing frequency.
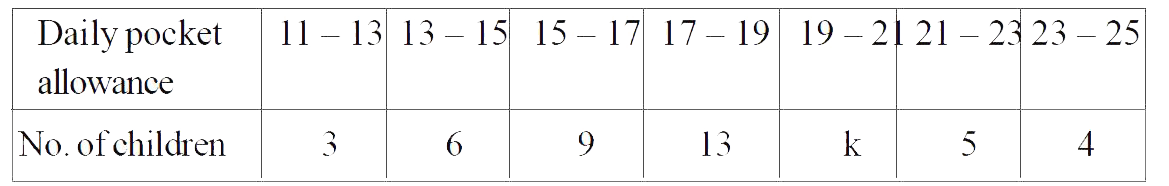
View SolutionThe following distribution shows the daily pocket allowance given to the children of a multistorey building. The average pocket allowance is Rs 18.00. Find out the missing frequency: Class 11-13 13-15 15-17 17-19 19-21 21-23 23-25 interval: Frequency: 7 6 9 13 - 5 4
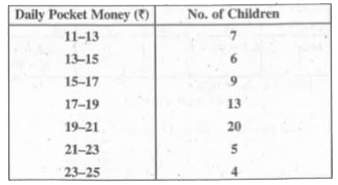
View SolutionThe following distribution shows the daily pocket money of children of a school.
Find the average daily pocket money of children.
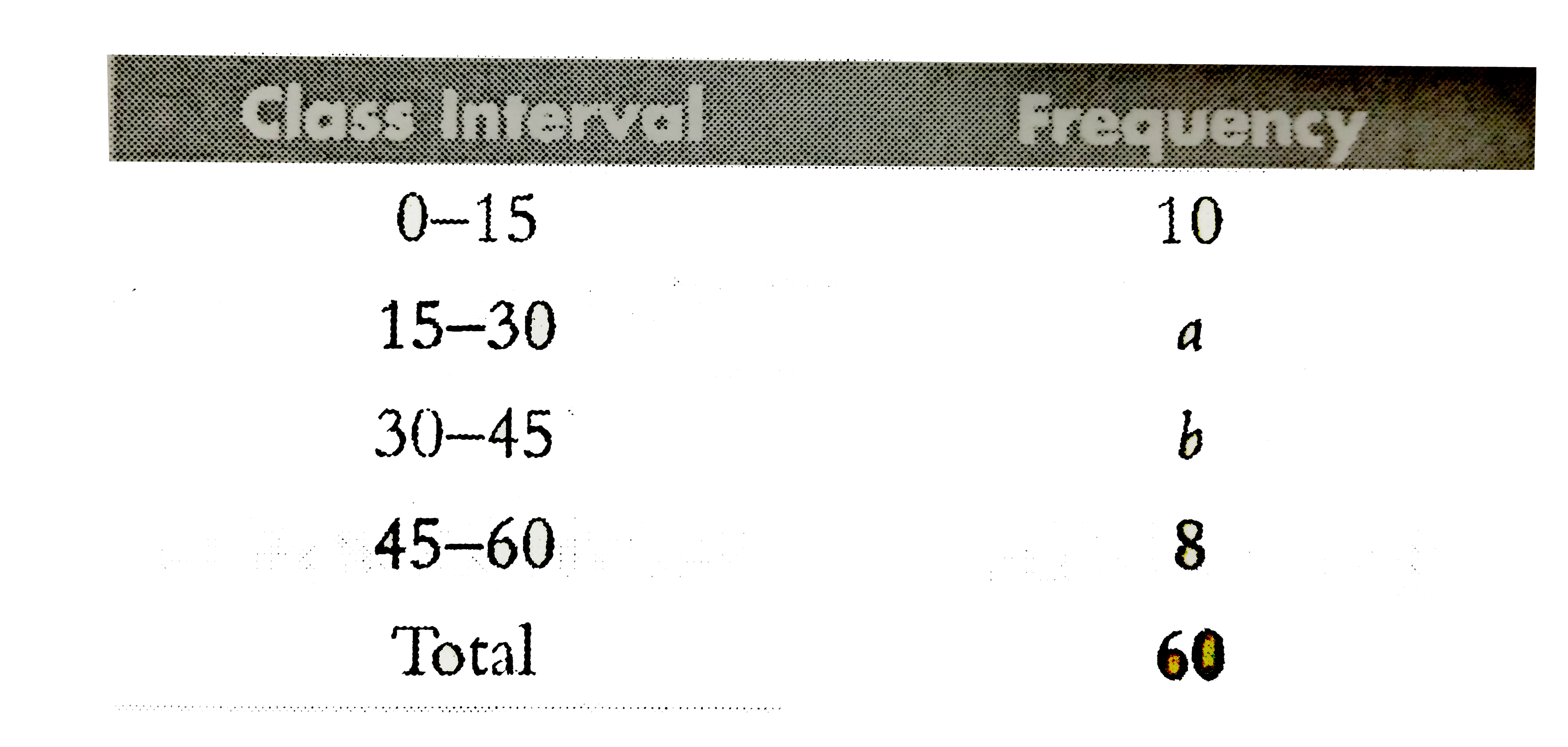
View SolutionIf the mean of the following table is 30 , then find the missing frequencies .
View SolutionIf the mean of the following distribution is 54 , find the missing frequency x :

View SolutionIf mean of the given distribution is 65.6 find the missing frequency.
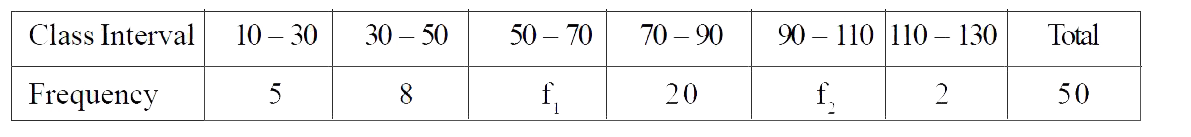
View SolutionThe mode of following frequency distribution is 36 . Find the missing frequency (f) .

View Solution
