Question

The function $f\left(x\right)=\frac{x}{1+x\tan x}$

Options

A. one point of minimum in the interval `(0,pi//2)`
B. one point of maxmimum `(0,pi//2)`
C. no points of maximum , no point of minimum in the interval `(0,pi//2)`
D. two points of maxima in the interval `(0,pi//2)`

Answer

B

Explanation

we have
`f(x) =(x)/(1+x tan x)`
`rArr f(x)=(1+ x tan x-x (tan x +x sec^2 x))/(1-x tan x)^2`
`rArr f(x) =(1-x^2sec^2x)/(1+tan x)^2`

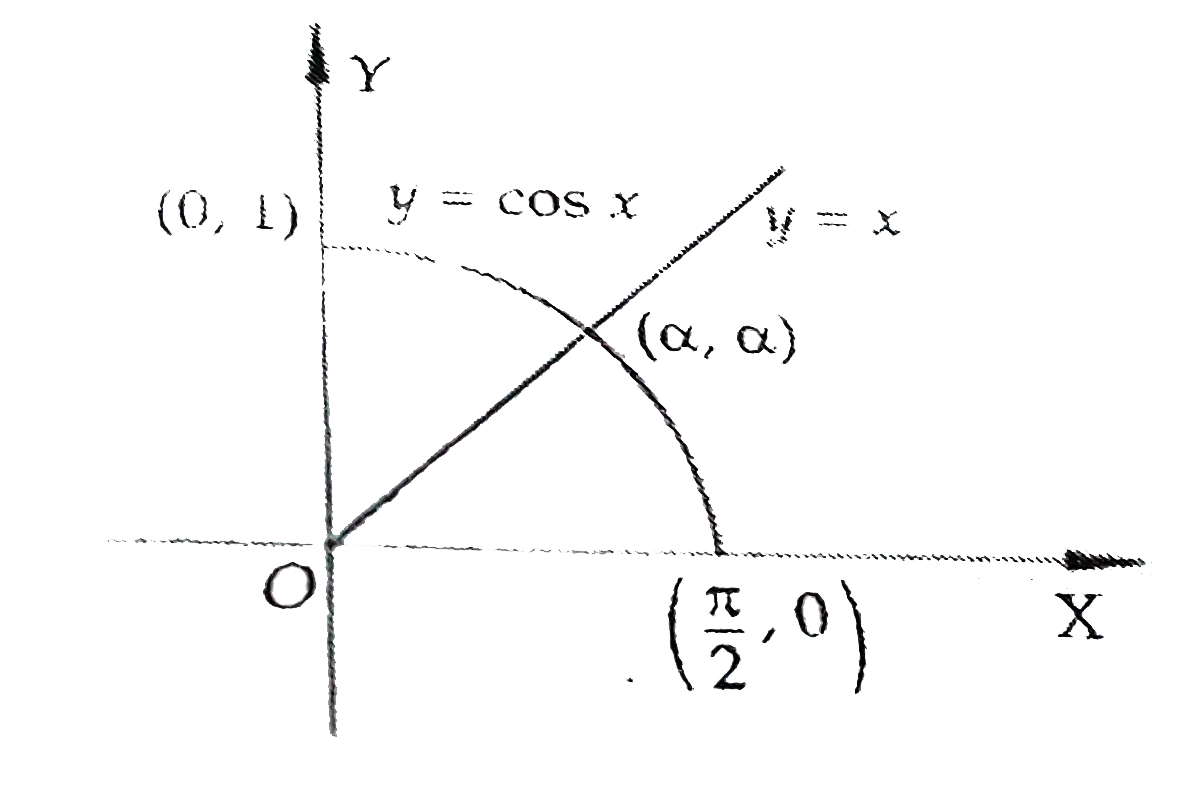
For local maximum of minmum , we must have
f'(x) =0
`rArr (1-x^2 sec ^2 x)/(1+x tan x )^2=0 rArr cos^2 x = x^2 rArr cos x = pm x `
`rArr cos x =x [ because ` x and cos x are positive for ` x in (0,pi//2)`
In order to find the number of solution of this equation ,let us draw the graphs of the curves y= cos x and y = x in `(0,pi//2)`
We find that the two curves intersect one point`(alpha, alpha)` only
`therefore f(x) =0 rArr cos alpha = alpha `
Now,
`f(x)=(1-x^2 sec ^2 x )/(1+ tan x)^2`
`rArr (1- x tan x)^2 f' (x) =1-x^2 sec^2 x`
`rArr (1+x tan x)^2 f'' (x)+2(1+ x tan x )(x sec ^2 x + tan x) f' (x)`
`= -2x sec^2 x -2x^2 sec ^2 x tan x`
`rArr (1+ alpha tan alpha)^2 f''(alpha) =-2 alpha sec^2 alpha - 2 alpha tan alpha `
`rArr f'' (alpha) lt 0.`
Therefore x = `alpha` is a point of local maximum
Hence , f(x) attains local maximum at one-point in the interval `(0,pi//2)`