The further the two regression lines cut each other, the …………. Be the degree of correlation.
The correct Answer is:lesser
To solve the question, "The further the two regression lines cut each other, the …………. Be the degree of correlation," we need to analyze the relationship between the distance of the regression lines and the degree of correlation.
1. Understanding Regression Lines:
- In statistics, regression lines are used to predict the value of one variable based on the value of another. The two regression lines typically considered are:
- Regression of Y on X (denoted as Y|X)
- Regression of X on Y (denoted as X|Y)
2. Properties of Regression Coefficients:
- The regression coefficients indicate the strength and direction of the relationship between the two variables.
- If the regression coefficient is zero, it indicates that there is no correlation between the variables, and the regression lines will be perpendicular to each other.
3. Correlation and Regression Lines:
- If the correlation is perfect (either positive or negative), the two regression lines will coincide, meaning they will overlap completely.
- If the correlation is weak, the regression lines will be further apart from each other.
4. Analyzing the Question:
- The question states that "the further the two regression lines cut each other," which implies that they are moving away from each other.
- This indicates a weaker correlation between the two variables.
5. Conclusion:
- Therefore, we can conclude that "the further the two regression lines cut each other, the lesser will be the degree of correlation."
Final Answer:
The further the two regression lines cut each other, the lesser will be the degree of correlation.
---
- In statistics, regression lines are used to predict the value of one variable based on the value of another. The two regression lines typically considered are:
- Regression of Y on X (denoted as Y|X)
- Regression of X on Y (denoted as X|Y)
- The regression coefficients indicate the strength and direction of the relationship between the two variables.
- If the regression coefficient is zero, it indicates that there is no correlation between the variables, and the regression lines will be perpendicular to each other.
- If the correlation is perfect (either positive or negative), the two regression lines will coincide, meaning they will overlap completely.
- If the correlation is weak, the regression lines will be further apart from each other.
- The question states that "the further the two regression lines cut each other," which implies that they are moving away from each other.
- This indicates a weaker correlation between the two variables.
- Therefore, we can conclude that "the further the two regression lines cut each other, the lesser will be the degree of correlation."
The further the two regression lines cut each other, the lesser will be the degree of correlation.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - QUESTION (STATE WHETHER THE FOLLOWING ARE TRUE OR FALSE)4videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - QUESTION (STATE GIVING REASONS, WHETHER EACH OF THE FOLLOWING STATEMENTS IS TRUE OR FALSE)10videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - QUESTION (PROBLEMS ON CORRELATION (State of nature of the following correlations) (positive, negative or no correlation))5videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test13videos
CONCEPTS OF SET THEORY
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)1videos
DEFINITE INTEGRAL
Similar Questions
Knowledge Check
- Question 1 - Select One
Calculate the coefficient of rank correlation.
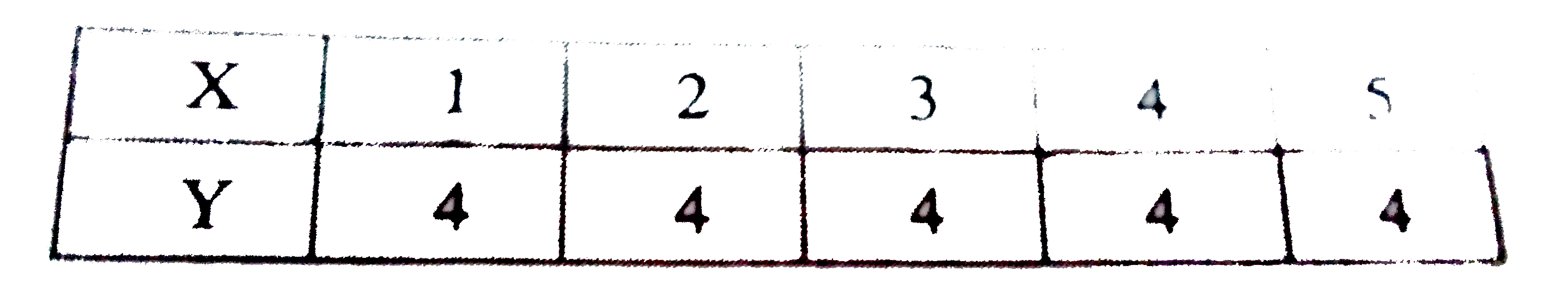 AOnly IB1 or -1COnly-1D0
AOnly IB1 or -1COnly-1D0 - Question 2 - Select One
Consider the following statements: 1 If the correlation coefficient rxy=0, then the two line of regression are parallel to each other r
2. If the correlation coefficient rxy=+1 then the two lines of regression are perpendicular to each other Which of the above statements are correct?A1onlyB2onlyCBoth I and IIDNeither I nor II - Question 3 - Select One
The regression lines will be perpendicular to each other if the coefficient of correlation r is equal to
A1 onlyB1 or −1C−1 onlyD0
The sign of regression coefficient is ………….. As that of correlation coefficient.
View SolutionConsider the following statements :
1. If the correlation coefficient rxy=0, then the two lines of regression are parallel to each other.
2. If the correlation coefficient rxy=±1, then the two lines of regression are perpendicular to each other.
Which of the above statements is/are correct?View SolutionThe two lines of regression meet at
View SolutionCan two isothermal curves cut each other
View SolutionThe regression line is obtained by
View Solution

