The graph of a polynomial P(x) cuts the x-axis at 3 points and touches it at 2 other points. The number of zeroes of P(x) is
1
2
3
5
To find the number of zeroes of the polynomial P(x), we need to analyze the information given about the graph of the polynomial.
1. Understanding the Graph Behavior: The problem states that the graph of the polynomial P(x) cuts the x-axis at 3 points. This means that at these points, the polynomial has distinct real roots (zeroes).
2. Counting the Cuts: Since the graph cuts the x-axis at 3 points, we can say that there are 3 zeroes contributed by these points.
3. Understanding Touch Points: The graph also touches the x-axis at 2 other points. When a polynomial touches the x-axis, it means that at these points, the polynomial has repeated roots. Each of these points contributes 1 zero, but since they are touch points, they are counted as double roots.
4. Counting the Touches: Since the graph touches the x-axis at 2 points, we can say that these contribute 2 more zeroes (each touch point counts as 1 zero).
5. Calculating Total Zeroes: Now, we can add the contributions from both the cuts and the touches:
- Zeroes from cuts: 3
- Zeroes from touches: 2
Therefore, the total number of zeroes of P(x) is:
3 (from cuts)+2 (from touches)=5
Thus, the number of zeroes of the polynomial P(x) is 5.
- Zeroes from cuts: 3
- Zeroes from touches: 2
3 (from cuts)+2 (from touches)=5
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-B
20 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- QUESTION PAPER 2022 TERM 1 SET 2 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 2 BASICEXERCISE - SECTION C (Case Study Based Question)
10 Videos
Similar Questions
Knowledge Check
Zero of the polynomial p(x)=2x+5 is
A−25B−52C25D52Zero of the polynomial p(x)=2x+5 is
A−25B−52C25D52The graph of polynomialp(x) is shown .
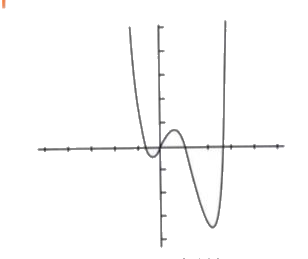
The number of zeroes of p(x) is :A3B4C5D6
What are the number of zeroes of p(x) for the given graph?
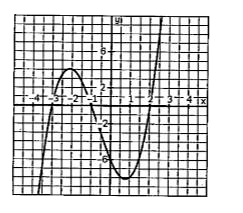
View Solution.The zeroes of the polynomial P(x)=x2−3x is
View SolutionThe zeroes of the polynomial p(x)=x2−3x are
View SolutionThe graph of a polynomial p(x) is given in the figure. What are the zeroes of the polynomial p(x) ?
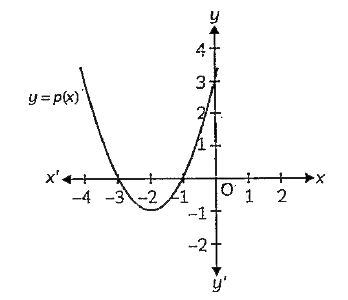
View SolutionThe zeros of the polynomial p(x)=x2−3x are
View Solution
