The graph of the derivative f'(x) is given in the following figure.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(d) Find the point of inflection.
From the graph ,f'<0 for x∈(0,1)∪(5,6) where f decreases.
From the graph, f'>0 for x∈(1,5) where f increases.
At x = 1, f ' changes sign from '-' to '+' , so it is the point of local minima.
At x = 5, f' changes sign from '+' to '-' , so it is the point of local maxima.
Slope of tangent to curve f' is '+' for x∈(0,3),i.e.f'>0.
Slope of tangent to curve f ' is '-' for x∈(3,6),i.e.f'<0.
That is , f'' changes sign at x = 3 with f''(3) = 0, so x = 3 is the point of inflection.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.241videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.251videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.221videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE ENGLISHCHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Graph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
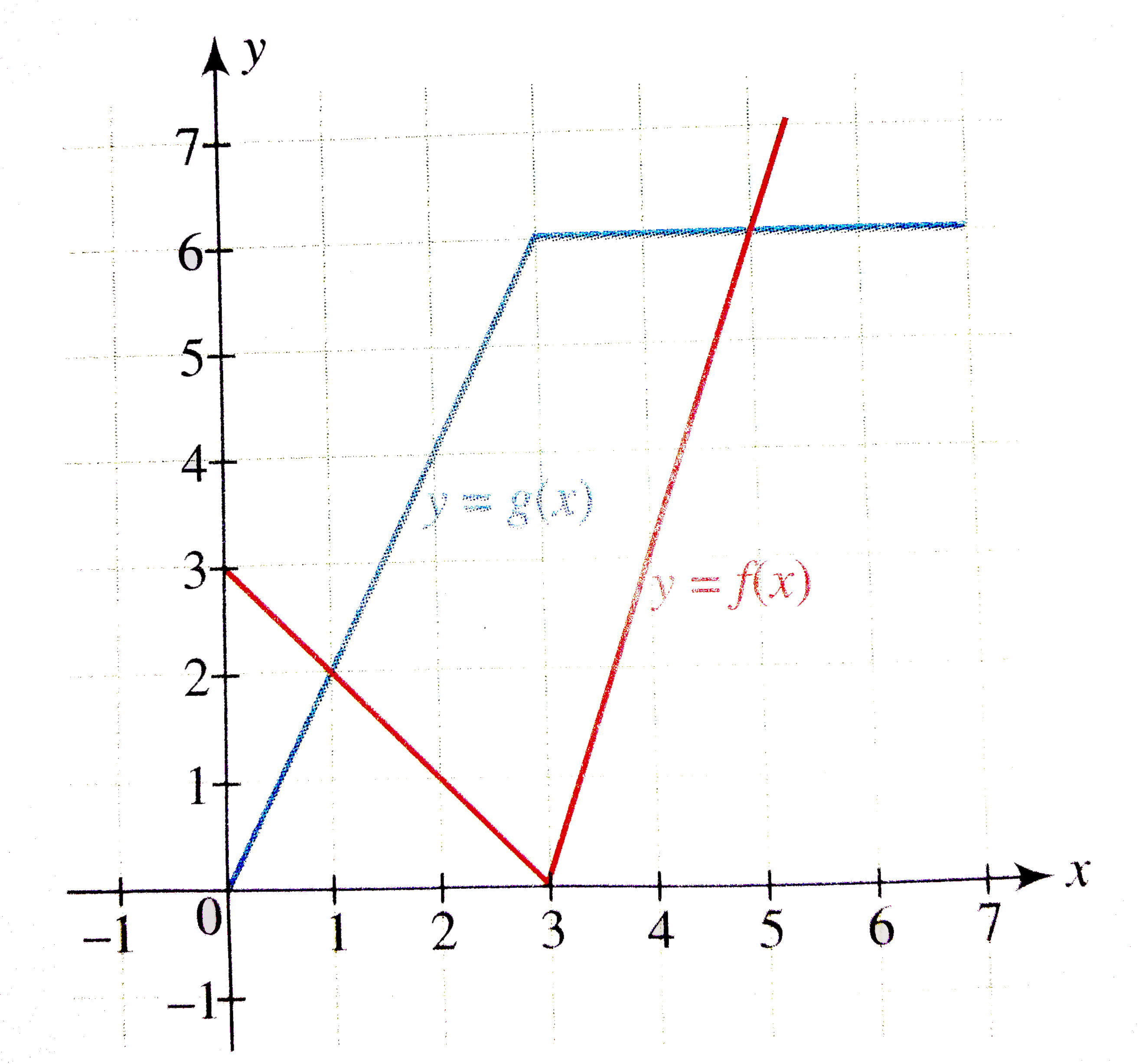View SolutionThe graph of a function is shown in the following figure.
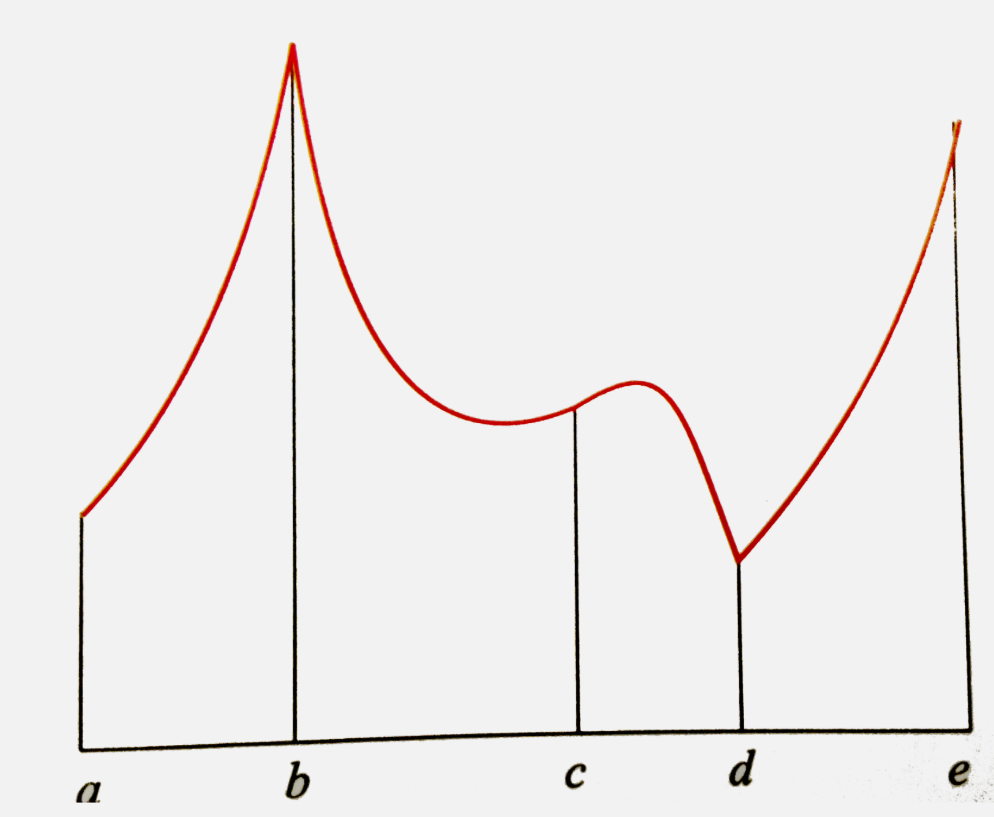
Determine the intervals on which the function is concave up and the intervals on which it is concave down. Find the x - coordinates of any inflection points.View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
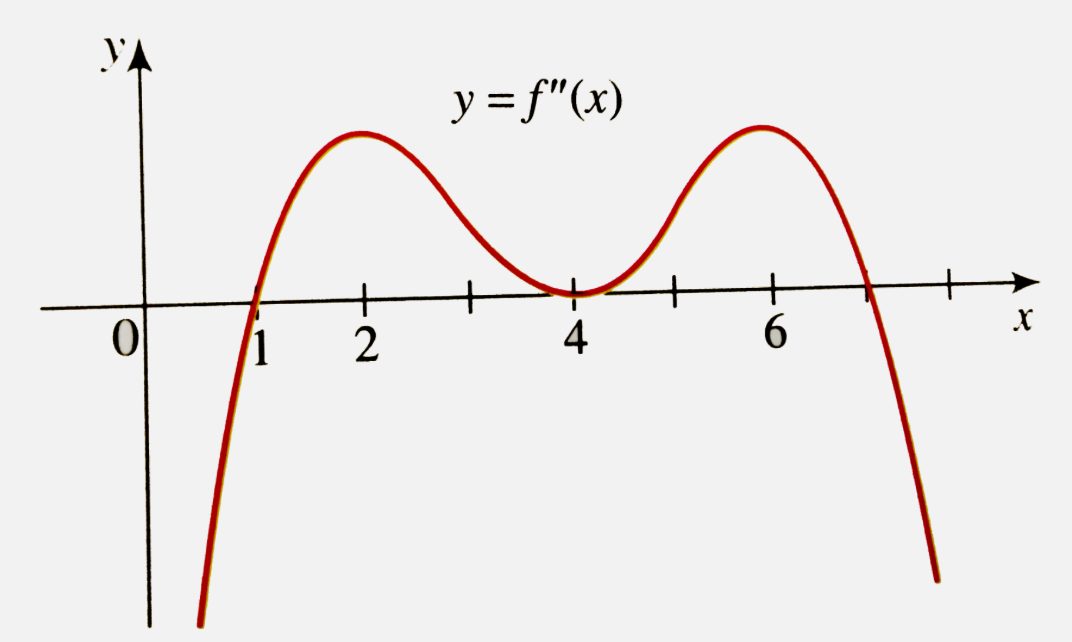View SolutionLet f(x)=x3 find the point at which f(x) assumes local maximum and local minimum.
View SolutionDraw the graph of f(x)=ln(1−ln x). Find the point of inflection.
View SolutionLet f(x)=x3−3x2+6 find the point at which f(x) assumes local maximum and local minimum.
View SolutionLet f(x)=x(x−1)2, find the point at which f(x) assumes maximum and minimum.
View SolutionFind the maximum and minimum values of f(x)=x+sin2x in the interval [0, 2π]
View SolutionFind the points of local maxima or local minima and corresponding local maximum and local minimum values of each of the given function. Also, find the points of inflection, if any : f(x)=xex
View SolutionDraw the graph of f(X)=loge(1−logex). Find the point of inflection
View Solution