The graph of y=6 is a line
parallel to X-axis at a distance 6 units from the origin
parallel to Y-axis at a distance 6 units from the origin
making an intercept 6 on the X-axis
making an intercept 6 on both axes
Given equation of line can be written as, 0.x+1.y=6
To draw the graph of above equation, we need atleast two solutions.
When x=0, then y=6
When x=2, then y=6

Here, we find two points A (0,6) and B(2,6). So, draw the graph, by plotting the points and joining the line AB.

Topper's Solved these Questions
- LINEAR EQUATION IN TWO VARIABLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR EQUATION IN TWO VARIABLESEXERCISE - Exercise 4.2
1 Videos
- LINEAR EQUATION IN TWO VARIABLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR EQUATION IN TWO VARIABLESEXERCISE - Exercise 4.3
11 Videos
- INTRODUCTION TO EUCLID GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions
5 Videos
- LINES AND ANGLES BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINES AND ANGLES EXERCISE - MULTIPLE CHOICE QUESTIONS
34 Videos
Similar Questions
Knowledge Check
The graph of line l in the xy-plane passes through the points (2,5)and(4,11). The graph of line m has a slope of -2 and an x-intercept of 2. If point (x, y) is the point of intersection of line l and m, what is the value of y?
A35B45C1D2Which of the following is the graph of a line perpendicular to the line defined by the equation 2x+5y=10?
A B
B C
C D
D
Draw the graph of straight line y=−2x+3 use your graph of find :
the area between the line and co-ordinates axes .
View SolutionThe graph of y=f(x) is given below
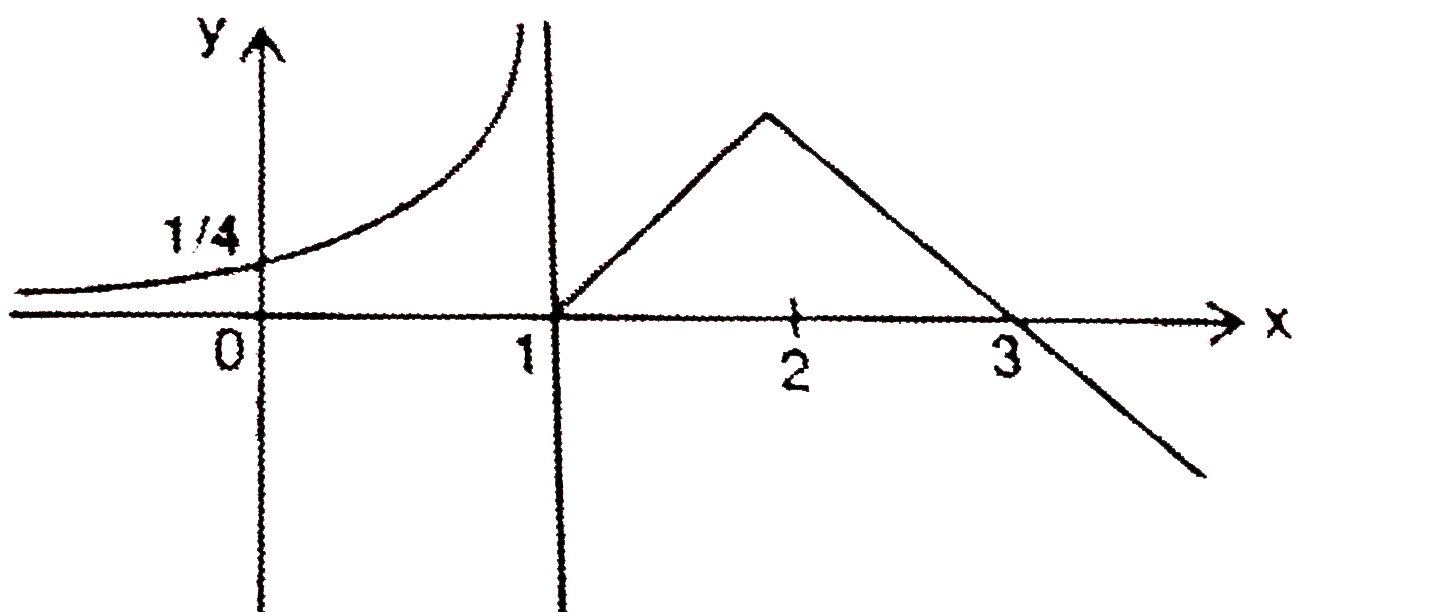
then the graph y=|f(|x|)| is :
View SolutionThe graph of the linear equation 2x+3y=6 is a line which meets the X-axis at the point.
View SolutionWe plot the graph having temperature in ∘C on x - axis and in ∘F on y - axis. If the graph is straight line, then the correct statement is
View SolutionIn the graph of y=2x and y=(12)x Which line is the axis of symmetry in the diagram?
View SolutionDraw the graphs of 2x+y=6andx−y+2=0. Shade the region boun-ded by these lines and x=axis. Find the area of the shaded region.
View Solution
