The greatest integral value of a such that √9−a2+2x−x2≥√16−x2 for at least one positive value of x is (a) 3 (b) 4 (c) 6 (d) 7
A
8
B
7
C
6
D
4
Video Solution
Text Solution
The correct Answer is:2
y=√9−a2+2ax−x2
y=√16−x2
⇒y2+(x−a)2=9
⇒y2+x2=16
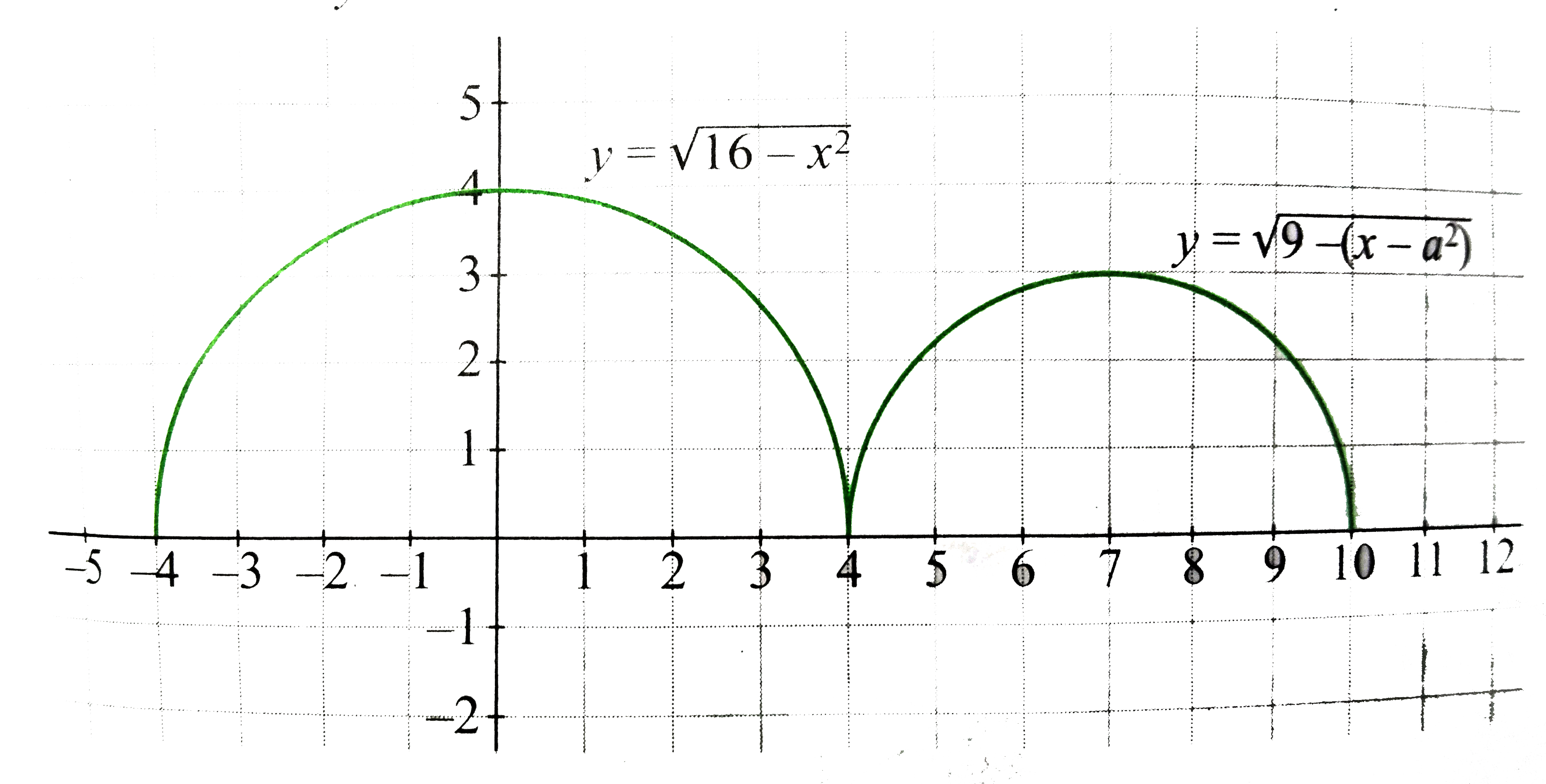
If a>7 , no solution exist, So, a≤7
Hence, maximum value of a is 7.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
The least integral value of x that satisfies 2x+4+3(x−5)>7 is
A3B4C5D6 - Question 2 - Select One
The greatest and the least value of the function, f(x)=√1−2x+x2−√1+2x+x2,x∈(−∞,∞) are
A2,-2B2,-1C2,0Dnone - Question 3 - Select One
If √3x−2=2√3+4, then the value of x is
A2(1−√3)B2(1+√3)C1+√3D1−√3
The value of (3+√2)(3−√2) is:
(a) 0 (b) 6 (c) 9 (d) 7View SolutionIf √3x−2=2√3+4, then the value of x is
View SolutionLeast integral value of (s) of a for which 4x−(a−2).2x+a<0 for at least one x in (0,∞) is (are)
View Solutionthe least value of 'a' for which the equation 2√asin2x+√a−3sin2x=5+√a has at least one solution is _______.
View SolutionIf 4:3=x2:12, then the value of x (x>0). 16 (b) 4 (c) 9 (d) 3
View Solution

